python求解三角形第三边长实例

目录
  • 求解三角形第三边长
  • python三角函数用法

求解三角形第三边长

import math
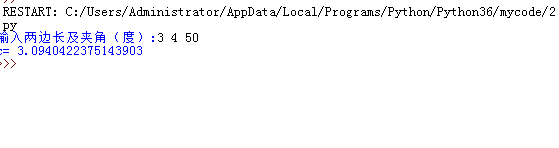
x=input('输入两边长及夹角（度）:')#输入时候使用空格分隔3个值
a,b,theta=map(float,x.split())#序列解包，split()方法用于切分字符串
c=math.sqrt(a**2+b**2-2*a*b*math.cos(theta*math.pi/180))
                    #cos()参数为弧度
print('c=',c)

运行截图

python三角函数用法

python中的三角函数一般有：

函数 描述
sin(x) 返回x弧度的正弦值
cos(x) 返回x弧度的余弦值
tan(x) 返回x弧度的正切值
asin(x) 返回x的反正弦弧度值
acos(x) 返回x的反余弦弧度值
atan(x) 返回x的反正切弧度值

上述三角函数的参数是：弧度！不是角度！

在数学和物理中，弧度是角的度量单位。

它是由国际单位制导出的单位，单位缩写是rad。定义：弧长等于半径的弧，其所对的圆心角为1弧度。

360°=2π弧度，因此，1弧度约为57.3°，即57°17’44.806"。

  • 1° = π/180弧度
  • 180° = π弧度

（在python中， pi = π，它是数学常量，引用时不要忘了math!）

在python中使用三角函数时，不能直接使用，要先导入math模块。

如下所示：

import math
a = math.cos(math.pi)    #求cos(180°)
b = math.sin(math.pi/2)  #求sin(90°）
print(a,b)
"""
输出：
-1.0  1.0  
"""

另外，在math模块中有两个函数：

  • degrees(x) : 将弧度转化为角度。
  • radians(x) : 将角度转化为弧度。

如下所示：

import math
a = math.degrees(math.pi/2)  
print(a)
b = math.radians(180)
print(b)
"""
输出:
90.0
3.141592653589793   180度的弧度是 π。
"""

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python打印三角形九九乘法表代码

    Python打印三角形九九乘法表代码

    正三角形九九乘法表 #正三角形九九乘法表 for i in range(1,10): for j in range(1,i+1): print(str(i)+"*"+str(j)+"="+str(i*j),end="\t") print("\n") 实现效果如下图所示: 倒三角形九九乘法表 #倒三角形九九乘法表 for m in range(1,10): for n in range(m,10): #print("{

  • python实现输入三角形边长自动作图求面积案例

    三角形是个好东西,比如知道三条边边长,可以判断能不能组成三角形(两边之和大于第三边),如果可以就进一步计算其面积(海伦公式),最后还能把这个三角形画出来(余弦定理求角度),所以说这个作为一个编程题目用于教学是比较棒的. 在jupyterlab中运行效果如下: python源代码如下: # %matplotlib inline # 建议在jupyterlab中运行 import math import numpy as np import matplotlib.pyplot as plt def

  • python 已知三条边求三角形的角度案例

    我就废话不多说了,还是直接看代码吧! import math a=1;//边1 b=1;//边2 c=math.sqrt(2);//边3 A=math.degrees(math.acos((a*a-b*b-c*c)/(-2*b*c)))//夹角1 B=math.degrees(math.acos((b*b-a*a-c*c)/(-2*a*c)))//夹角2 C=math.degrees(math.acos((c*c-a*a-b*b)/(-2*a*b)))//夹角3 print(A) print(B

  • 使用Python三角函数公式计算三角形的夹角案例

    题目内容: 对于三角形,三边长分别为a, b, c,给定a和b之间的夹角C,则有:.编写程序,使得输入三角形的边a, b, c,可求得夹角C(角度值). 输入格式: 三条边a.b.c的长度值,每个值占一行. 输出格式: 夹角C的值,保留1位小数. 输入样例: 3 4 5 输出样例: 90.0 code: import math a = float(eval(input('请输入a的边长'))) b = float(eval(input('请输入b的边长'))) c = float(eval(in

  • 使用python计算三角形的斜边例子

    我就废话不多说了,还是直接看代码吧 def c(a,b): c=a**2+b**2 return ("the right triangle third side's length is"+" " + str(c)) c(3,4) 注:中间的空格符是一对引号加一个空格 补充知识:三角形已知两边一斜角时求第三边的公式 已知三角形中的一个角θ \thetaθ和其对边b bb以及侧边a aa, 第三条边长的计算公式为 证明很简单, 用海伦公式和三角形两边一内角的面积公式,

  • Python3如何判断三角形的类型

    # 判断三角形类型 def triangle(a,b,c): if a>0 and b>0 and c>0: if a+b>c and b+c>a and a+c>b: if a == b and b == c: return ("这是等边三角形") elif a == b or b == c or c == a: return("这是等腰三角形") else: return("这是不规则三角形") elif

  • python求解三角形第三边长实例

    python求解三角形第三边长实例

    目录 求解三角形第三边长 python三角函数用法 求解三角形第三边长 import math x=input('输入两边长及夹角(度):')#输入时候使用空格分隔3个值 a,b,theta=map(float,x.split())#序列解包,split()方法用于切分字符串 c=math.sqrt(a**2+b**2-2*a*b*math.cos(theta*math.pi/180)) #cos()参数为弧度 print('c=',c) 运行截图 python三角函数用法 python中的三角

  • Python中逗号的三种作用实例分析

    本文实例讲述了Python中逗号的三种作用.分享给大家供大家参考.具体分析如下: 最近研究python  遇到个逗号的问题 一直没弄明白 今天总算搞清楚了 1.逗号在参数传递中的使用: 这种情况不多说  没有什么不解的地方 就是形参或者实参传递的时候参数之间的逗号 例如def  abc(a,b)或者abc(1,2) 2.逗号在类型转化中的使用 主要是元组的转换 例如: >>> a=11 >>> b=(a) >>> b 11 >>> b

  • python组合无重复三位数的实例

    # -*- coding: utf-8 -*- # 简述:这里有四个数字,分别是:1.2.3.4 #提问:能组成多少个互不相同且无重复数字的三位数?各是多少? def f(n): list=[] count=0 for i in range(1,n+1): for j in range(1, n+1): for k in range(1, n+1): if i!=j and j!=k and i!=k: list.append(i*100+j*10+k) count=len(list) prin

  • Python求解排列中的逆序数个数实例

    在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序. 一个排列中逆序的总数就称为这个排列的逆序数. 一个排列中所有逆序总数叫做这个排列的逆序数. 也就是说,对于n个不同的元素,先规定各元素之间有一个标准次序(例如n个 不同的自然数,可规定从小到大为标准次序),于是在这n个元素的任一排列中,当某两个元素的先后次序与标准次序不同时,就说有1个逆序. 一个排列中所有逆序总数叫做这个排列的逆序数. Python代码: def inverse_number(s

  • python 图像插值 最近邻、双线性、双三次实例

    最近邻: import cv2 import numpy as np def function(img): height,width,channels =img.shape emptyImage=np.zeros((2048,2048,channels),np.uint8) sh=2048/height sw=2048/width for i in range(2048): for j in range(2048): x=int(i/sh) y=int(j/sw) emptyImage[i,j]

  • 使用python求解迷宫问题的三种实现方法

    使用python求解迷宫问题的三种实现方法

    目录 前言 递归求解 回溯求解 队列求解 总结 前言 在迷宫问题中,给定入口和出口,要求找到路径.本文将讨论三种求解方法,递归求解.回溯求解和队列求解. 在介绍具体算法之前,先考虑将迷宫数字化.这里将迷宫用一个二维的list存储(即list嵌套在list里),将不可到达的位置用1表示,可到达的位置用0表示,并将已经到过的位置用2表示. 递归求解 递归求解的基本思路是: 每个时刻总有一个当前位置,开始时这个位置是迷宫人口. 如果当前位置就是出口,问题已解决. 否则,如果从当前位置己无路可走,当前的

  • Python实现绘制多角星实例

    Python实现绘制多角星实例

    目录 一.引言 二.方法 三.实验结果与讨论 1.三角形的绘制 2.五角星的绘制 3.多角星的绘制 四. 结语 本文转自微信公众号:算法与编程之美 一.引言 在具备一定的Python编程基础以后,我们可以结合for循环进行多角星的编写,只要简单的几次循环,即可以极大的解决重复编写相同代码方面的问题,下面小编将以三角星.五角星为例,进而引入如何绘制多角星. 二.方法 预备知识: 命令 说明 pensize(width) 设置画笔宽度 turtle.forward(distance) 向画笔方向移动

  • python 已知平行四边形三个点,求第四个点的案例

    我就废话不多说了,大家还是直接看代码吧! import numpy as np #已知平行四边形三个点,求第四个点 #计算两点之间的距离 def CalcEuclideanDistance(point1,point2): vec1 = np.array(point1) vec2 = np.array(point2) distance = np.linalg.norm(vec1 - vec2) return distance #计算第四个点 def CalcFourthPoint(point1,p

  • python求解汉诺塔游戏

    本文实例为大家分享了python求解汉诺塔游戏的具体代码,供大家参考,具体内容如下 一.问题定义 百度百科定义:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.据说大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照从小到大顺序摞着64片黄金圆盘.大梵天命令婆罗门借助其中一根柱子,把64片黄金圆盘重新摆放到第三个根柱子上.并且规定,在小黄金圆盘上不能放大的黄金圆盘,在三根柱子之间一次只能移动一个圆盘. 例如,如果黄金圆盘只有3片,则为了满足游戏规则,那么必须按照如下图所示的

随机推荐