有意思的数据结构默克树 Merkle tree应用介绍

目录
  • 一种有意思的数据结构-默克树（Merkle tree）
    • 长什么样子？
  • Hash链表
    • 防篡改
  • 判断某个交易是否被记录（是否存在）
  • 常见应用 - 1 git
  • 常见应用 - 2 分布式数据存储的数据校验
  • 小结

一种有意思的数据结构-默克树（Merkle tree）

默克树（Merkle tree）又叫hash树。程序员可以说自己不知道默克树，但是不能保证自己一定没有用过，因为git存储我们每一个版本代码和提交记录关系的数据结构就是默克树。

其在区块链技术中起着十分重要的作用，本文会介绍这种数据结构，并举例两个常见的应用场景（可能不够严谨）。

长什么样子？

下图是一个简单的默克树，可以看到除最底层的数据外，其他节点都是左右两个子节点的hash值组成。（注：红线代表左右顺序）

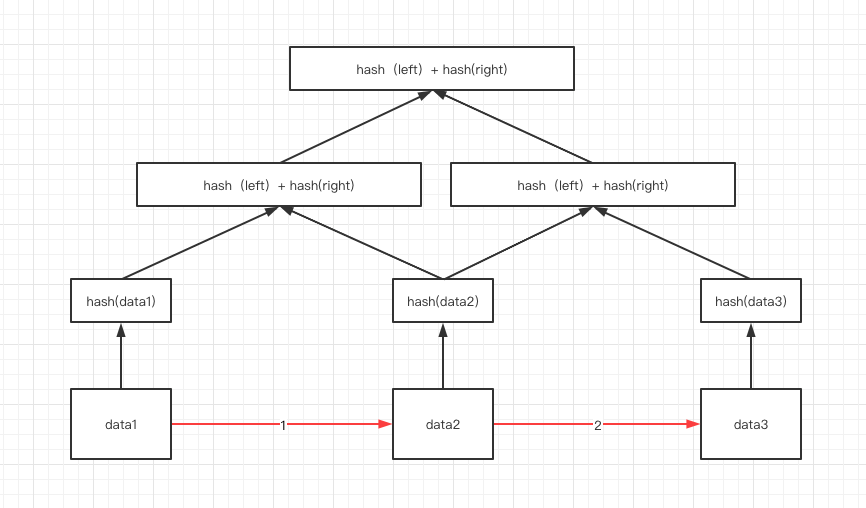
Hash链表

链表的定义就是当前节点指向下一个节点，传统链表是使用地址作为指向，但是区块链中的链表和默克树一样，使用上一个节点的hash值作为指向，如图：

防篡改

这两种数据结构天生就具备防篡改的特性，我们看他们在区块链中的形态：

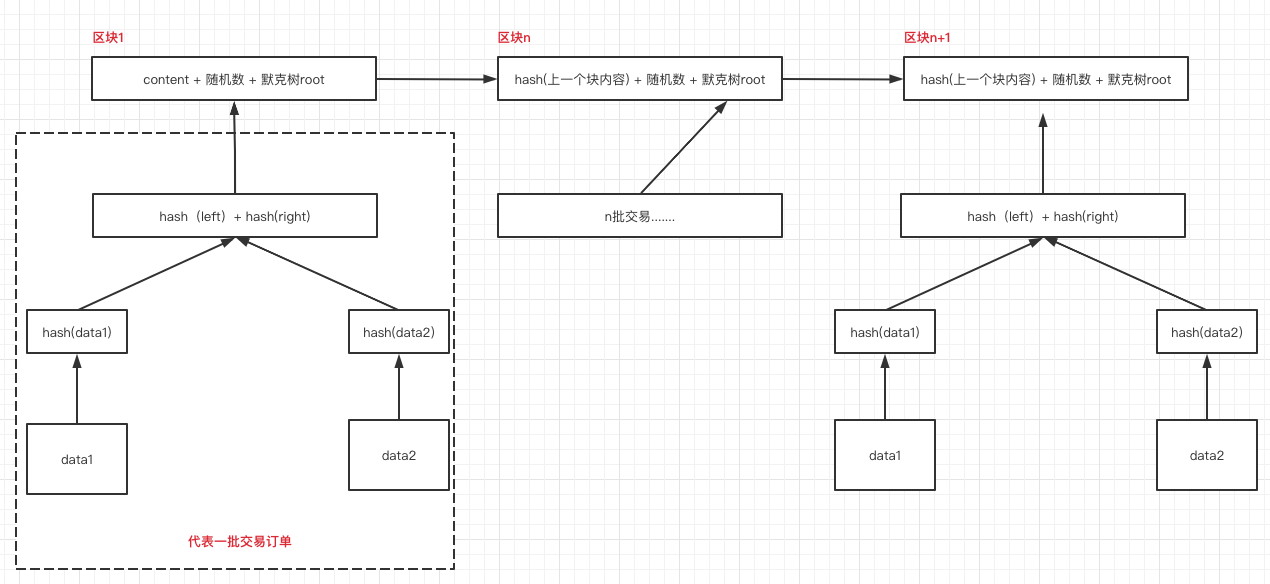
假设我们更改了左边虚框内那一批已经存在的交易数据，例如data1，那区块1的默克树root值就一定会改变，区块1的hash值也一定会变，这种变化会产生新的链，当发现这条新链在区块1后的所有区块值与各个节点原本记录的值不一致，就会认为有人修改了链上的旧数据。

而且我们使用的是hash值作为指向，只要大家手上的最后一个值没问题，在回溯时必然无法回溯到被篡改的数据，甚至回溯对比后还可以知道哪里发生了篡改。

既然无法指向我们篡改的数据，那我们把后面的所有区块以及其数据也篡改了行不行？可以的，但是区块有无数个，而且并不是简单的遍历修改本地数据就ok了，还需要所有节点的共识，你能黑光所有的节点，让他们都直接放弃手中的数据，认可你这新的链吗？

所以在对账时，就很容易知道账目是否正确，由于是直接比较hash值，使用默克树去判断内容是否被篡改是很快的！

我们看看默克树在分布式记账的应用中是如何大展身手的！！

判断某个交易是否被记录（是否存在）

你怎么保证你手中的数据和链上一致？怎么证明你的数据在链上呢？

例子：你在银行存了50万，银行怎么证明它给你存了50万呢？

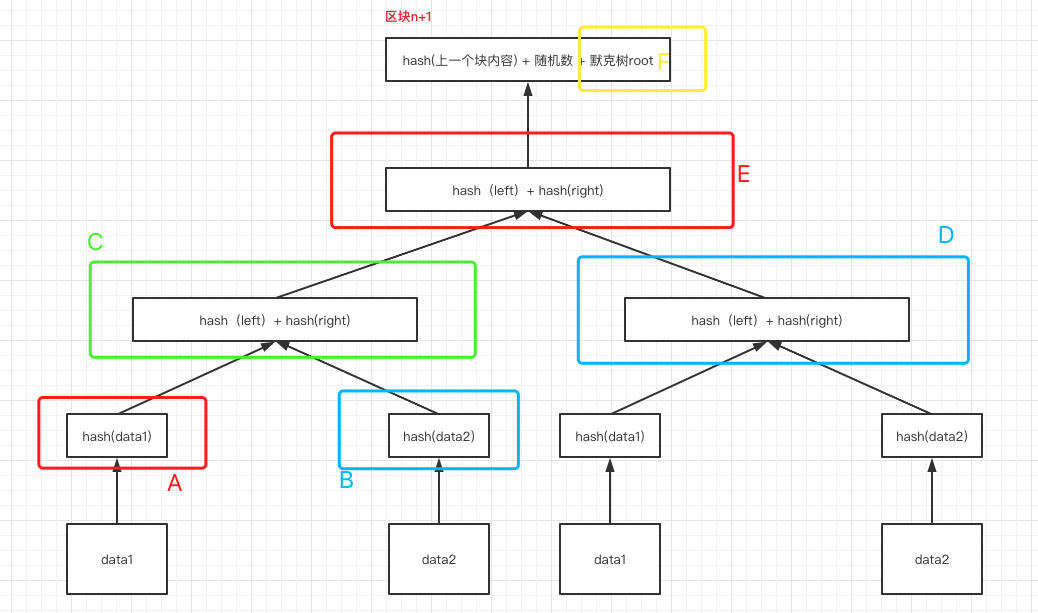
1.我们首先要向信任节点获取蓝色框和黄色框的值。

2.这里假设我们判断data1数据，算出我们要判断的数据的记为A，A与B进行hash,得到C

3.将C与D进行hash，得到E

4.判断E是否等于 F，等于说明存在。

常见应用 - 1 git

我们切换commit时，git是怎么实现不同commit文件数量和文件内容的切换的？

git会记录所有版本的文件，例如文件a在第一个commit中内容是1，第二次commit中内容是2，此时git本地仓库中会分别有：内容为1的文件a，内容为2的文件a。

git中每一个commit就相当于一个区块，这个区块有对应的默克树，而默克树中的hash值又指向了对应的文件，所以切换一个commit其实就相当于将当前区块切换，如下图：

注：将工作区的文件改成本地仓库的某个版本的文件是index区负责的，这里就不细讲了。

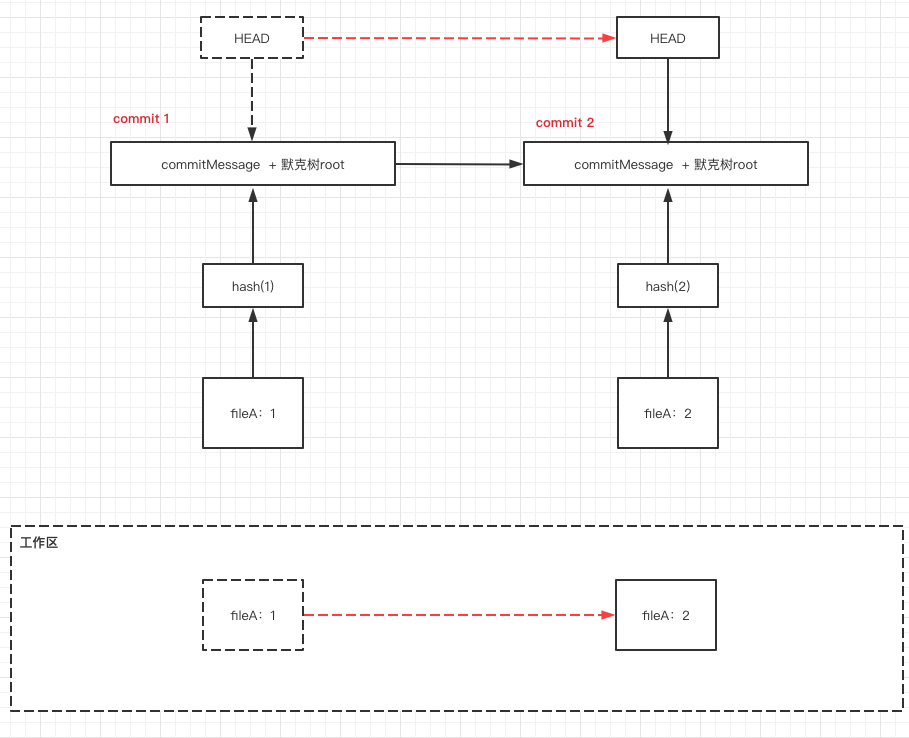
常见应用 - 2 分布式数据存储的数据校验

我们将成千上万个文件存在互联网上的任意服务器，任何一个能上网的终端，都可以作为我们的存储器，注：假设我们为了保证性能，不通过中介服务器，直接p2p连接，并且不校验这些存储器的身份。那如何保证我们从这些不受信任的存储器中下载的数据，是我们存入时的样子（没有被篡改）？

是否可以尝试如下步骤：

0.这些任意的服务器都要拥有其存储文件的默克树。

1.终端下载这个服务器中存储的默克树，向值得信任的服务器取得这个默克树对应区块的值，计算并判断默克树顶部的hash值是否等于区块记录的值，等于说明这个服务器记录的默克树没有问题。

下面两步任选一个都能确认文件没被篡改。

2.使用时判断这个文件内容是否有被这个默克树记录。

3.判断所有文件都被这个默克树记录。

小结

可以看到默克树的根本在于hash的计算，是否真的能保证防篡改呢？，如果想进一步了解，可以看看密码学中有关于Collision resistance（抗碰撞性）和 Hiding（隐藏性）。

也可以看：密码学基础.md

以上就是有意思的数据结构默克树 Merkle tree应用介绍的详细内容，更多关于数据结构默克树 Merkle tree的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • Redis 哈希Hash底层数据结构详解

    Redis 哈希Hash底层数据结构详解

    目录 1. Redis 底层数据结构 2. hashtable 3. redisDb 与 redisObject 4. ziplist 5. linkedlist 6. quicklist 1. Redis 底层数据结构 Redis数据库就像是一个哈希表,首先对key进行哈希运算得到哈希值再取模得到一个下标,每个元素是一个节点,节点之间形成链表.这感觉有点像Java中的HashMap. 不同的数据类型的实现方式是不一样的,可以通过object encoding命令查看底层真正的数据存储结构 同一

  • Go语言数据结构之希尔排序示例详解

    Go语言数据结构之希尔排序示例详解

    目录 希尔排序 算法思想 图解算法 Go 代码实现: 总结 希尔排序 在插入排序中,在待排序序列的记录个数比较少,而且基本有序,则排序的效率较高. 1959 年,Donald Shell 从“减少记录个数” 和 “基本有序” 两个方面对直接插入排序进行了改进,提出了希尔排序算法. 希尔排序又称为“缩小增量排序”.即将待排序记录按下标的一定增量分组(减少记录个数),对每组记录使用直接插入排序算法排序(达到基本有序): 随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1,整个序列基本有序,再对

  • 详解Pytorch中的tensor数据结构

    详解Pytorch中的tensor数据结构

    目录 torch.Tensor Tensor 数据类型 view 和 reshape 的区别 Tensor 与 ndarray 创建 Tensor 传入维度的方法 torch.Tensor torch.Tensor 是一种包含单一数据类型元素的多维矩阵,类似于 numpy 的 array.Tensor 可以使用 torch.tensor() 转换 Python 的 list 或序列数据生成,生成的是dtype 默认是 torch.FloatTensor. 注意 torch.tensor() 总是

  • C++数据结构之二叉搜索树的实现详解

    C++数据结构之二叉搜索树的实现详解

    目录 前言 介绍 实现 节点的实现 二叉搜索树的查找 二叉搜索树的插入 二叉搜索树的删除 总结 前言 今天我们来学一个新的数据结构:二叉搜索树. 介绍 二叉搜索树也称作二叉排序树,它具有以下性质: 非空左子树的所有键值小于其根节点的键值 非空右子树的所有键值大于其根节点的键值 左,右子树都是二叉搜索树 那么我先画一个二叉搜索树给大家看看,是不是真的满足上面的性质. 我们就以根节点6为例子来看,我们会发现比6小的都在6的左边,而比6大的都在6的右边.对于6的左右子树来说,所有的节点都遵循这个规则.

  • 有意思的数据结构默克树 Merkle tree应用介绍

    有意思的数据结构默克树 Merkle tree应用介绍

    目录 一种有意思的数据结构-默克树(Merkle tree) 长什么样子? Hash链表 防篡改 判断某个交易是否被记录(是否存在) 常见应用 - 1 git 常见应用 - 2 分布式数据存储的数据校验 小结 一种有意思的数据结构-默克树(Merkle tree) 默克树(Merkle tree)又叫hash树.程序员可以说自己不知道默克树,但是不能保证自己一定没有用过,因为git存储我们每一个版本代码和提交记录关系的数据结构就是默克树. 其在区块链技术中起着十分重要的作用,本文会介绍这种数据结

  • Java数据结构学习之树

    Java数据结构学习之树

    一.树 1.1 概念 与线性表表示的一一对应的线性关系不同,树表示的是数据元素之间更为复杂的非线性关系. 直观来看,树是以分支关系定义的层次结构. 树在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构都可以用树的形象来表示. 简单来说,树表示的是1对多的关系. 定义(逻辑结构): 树(Tree)是n( n>=0 )个结点的有限集合,没有结点的树称为空树,在任意一颗非空树中: 有且仅有一个特定的称为根(root)的结点 . 当n>1的时,其余结点可分为 m( m>0 ) 个互不相交的

  • C++高级数据结构之线段树

    目录 前言: 高级数据结构(Ⅲ)线段树(Segment Tree) 线段树的原理 树的创建 单点修改 区间查找 完整代码及测试 前言: 高级数据结构(Ⅲ)线段树(Segment Tree) 线段树的原理 树的创建 单点修改 区间查找 完整代码及测试 高级数据结构(Ⅲ)线段树(Segment Tree) 线段树的原理 线段树是一种二叉搜索树 , 对于线段树中的每一个非叶子结点[a,b],它的左儿子表示的区间为[a, (a+b)/2],右儿子表示的区间为[(a+b)/2+1, b].因此线段树是平衡

  • 数据结构之伸展树详解

    数据结构之伸展树详解

    1. 概述 二叉查找树(Binary Search Tree,也叫二叉排序树,即Binary Sort Tree)能够支持多种动态集合操作,它可以用来表示有序集合.建立索引等,因而在实际应用中,二叉排序树是一种非常重要的数据结构. 从算法复杂度角度考虑,我们知道,作用于二叉查找树上的基本操作(如查找,插入等)的时间复杂度与树的高度成正比.对一个含n个节点的完全二叉树,这些操作的最坏情况运行时间为O(log n).但如果因为频繁的删除和插入操作,导致树退化成一个n个节点的线性链(此时即为一个单链表

  • C语言数据结构之中缀树转后缀树的实例

    C语言数据结构之中缀树转后缀树的实例 对于一个中缀表达式 a+b*c*(d-e/f) 转换成后缀是这样的形式 abc*def/-+ 后缀表达式是相当有用处的,转换成后缀表达式后求值会简单很多.那么该如何转换呢? 网上关于这方面的资料一搜一大把,每本数据结构的书中都会提及这个算法,在这个算法中,用到 栈 这个数据结构. 1,关键是比较运算符的优先级,谁的优先级高,谁就出现在前面上面的表达式中,有括号的时候括号优先级最高,*/次之,+-最后. 在上面的表达式中+的优先级不如*的高,因此,在后缀表达式

  • MySQL底层数据结构选用B+树的原因

    MySQL底层数据结构选用B+树的原因

           我们都知道MySQL底层数据结构是选用的B+树,那为什么不用红黑树,或者其他什么数据结构呢?         红黑树是一种自平衡二叉查找树,Java8中的hashmap就用到红黑树来优化它的查询效率,可见,红黑树的查询效率还是比较高的,但是为什么MySQL的底层不用红黑树而用B+数呢?         下图是红黑树依次插入1,2,3,4,5,6之后的情况:  然后再在上面的红黑树中插入7:        可以看到,尽管红黑树经过了自平衡,数据整体仍然偏向树的右侧,如果继续添加更多数

  • Java数据结构之线段树详解

    Java数据结构之线段树详解

    目录 介绍 代码实现 线段树构建 区间查询 更新 总结 介绍 线段树(又名区间树)也是一种二叉树,每个节点的值等于左右孩子节点值的和,线段树示例图如下 以求和为例,根节点表示区间0-5的和,左孩子表示区间0-2的和,右孩子表示区间3-5的和,依次类推. 代码实现 /** * 使用数组实现线段树 */ public class SegmentTree<E> { private Node[] data; private int size; private Merger<E> merge

  • C++数据结构之AVL树的实现

    C++数据结构之AVL树的实现

    目录 1.概念 (1)二叉搜索树的缺点 (2)定义节点 2.插入 (1)拆分 (2)找节点与插节点 (3)更新平衡因子与旋转 3.判断 4.完整代码及测试代码 完整代码 测试代码 1.概念 (1)二叉搜索树的缺点 要手撕AVL树,我们首先要知道什么是AVL树.AVL树是在二叉搜索树的基础之上改造的.当我们插入的是一个有序的序列的时候,二叉搜素树会使用一条直线来进行存储,这样并不利于查找. 当遇到这种情况的时候我们就需要对这棵树来进行调整.AVL树会通过旋转等操作,来规避这种情况.最终满足每一个节

  • Java数据结构之线段树的原理与实现

    Java数据结构之线段树的原理与实现

    目录 简介 实现思路 节点定义 构建线段树 求解区间和 更新线段树 简介 线段树是一种二叉搜索树,是用来维护区间信息的数据结构.可以在O(logN)的时间复杂度内实现单点修改.区间修改.区间查询(区间求和,求区间最大值,求区间最小值)等操作.接下来我以实现区间求和为例子来讲解线段树(最大值和最小值与求和实现方式几乎无异),假设存在一个数组[1,4,6,3,9]. 实现思路 从线段树的定义,我们首先需要定义一个树节点,节点包含区间和(23),区间([1-5]),左节点,右节点等.(如果要实现求区间

  • go语言数据结构之前缀树Trie

    go语言数据结构之前缀树Trie

    目录 介绍 流程 代码 初始化 插入 查找 统计以XXX开头的单词个数 删除数据 介绍 Trie树:又称为单词查找树,是一种树形结构,可以应用于统计字符串,会在搜索引擎系统中用于对文本的词频统计,下图是一个Trie树的结构,同时它也是在插入数时的一个顺序图. 流程 首先应该先创建一个结构体,里面保存的是每一个节点的信息 初始化根节点,根节点应该初始化啥?啥也不用初始化,给个空就好看上图 插入:串转字符数组:遍历数组,如果下一个节点为空,创建,则继续遍历 查找:串转字符数组,遍历如何所有字符都在树

随机推荐