c#二叉树存储介绍
目录
- 存储结构
- 二叉树的遍历
存储结构
二叉树是一种特殊的树,给个结点最多有两个子节点,并且子节点有左右之分,并且兄弟,父亲,孩子可以很方便的通过编号得到
1.在二叉树的第i层上最多有2i-1个结点(i>=1)
2.深度为k的二叉树至多有2i-1个结点
3.对于一个二叉树,假设它有n个结点,对结点进行从1开始编号,对任一结点i满足下面
a.它的双亲是节点i/2(除了i=1的情况)
b.左孩子是2i,右孩子是2i+1
c.如果2i>i说明无左孩子 2i+1>n说明无右孩子
二叉树的遍历
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中的所有结点,使每个结点被访问一次且仅被访问一次
1.前序遍历
先输出当前结点的数据,再依次遍历输出左结点和右结点
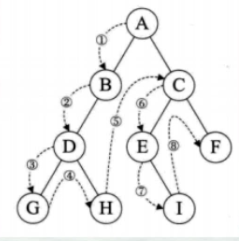
2.中序遍历
先遍历输出左结点,再输出当前结点的数据,再遍历输出右结点
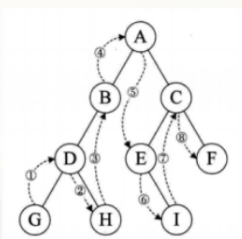
3.后序遍历
先遍历输出左结点,再遍历输出右结点,最后输出当前结点的数据
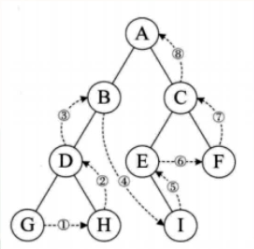
4.层序遍历
从树的第一层开始,从上到下逐层遍历,再同一层中,从左到右对结点逐个访问输出
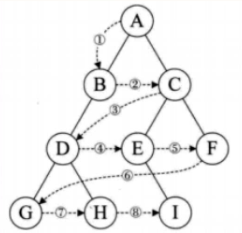
以下代码可以在c#中实现遍历
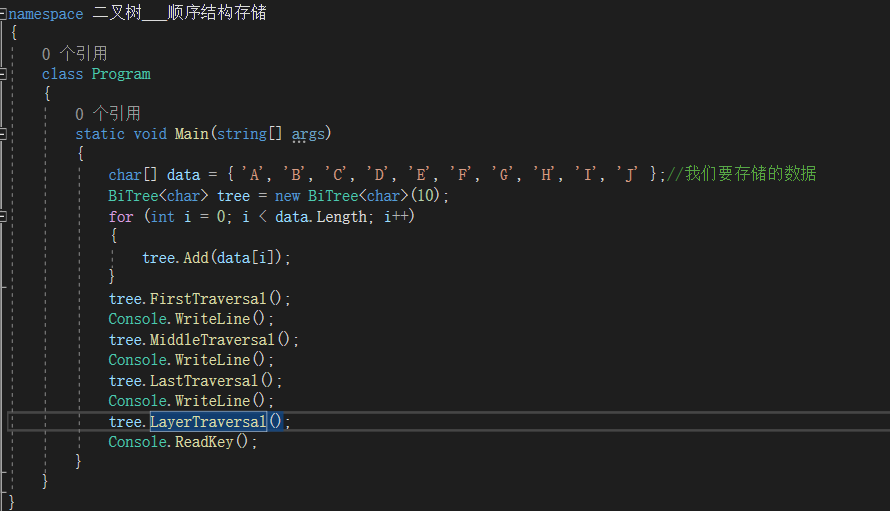
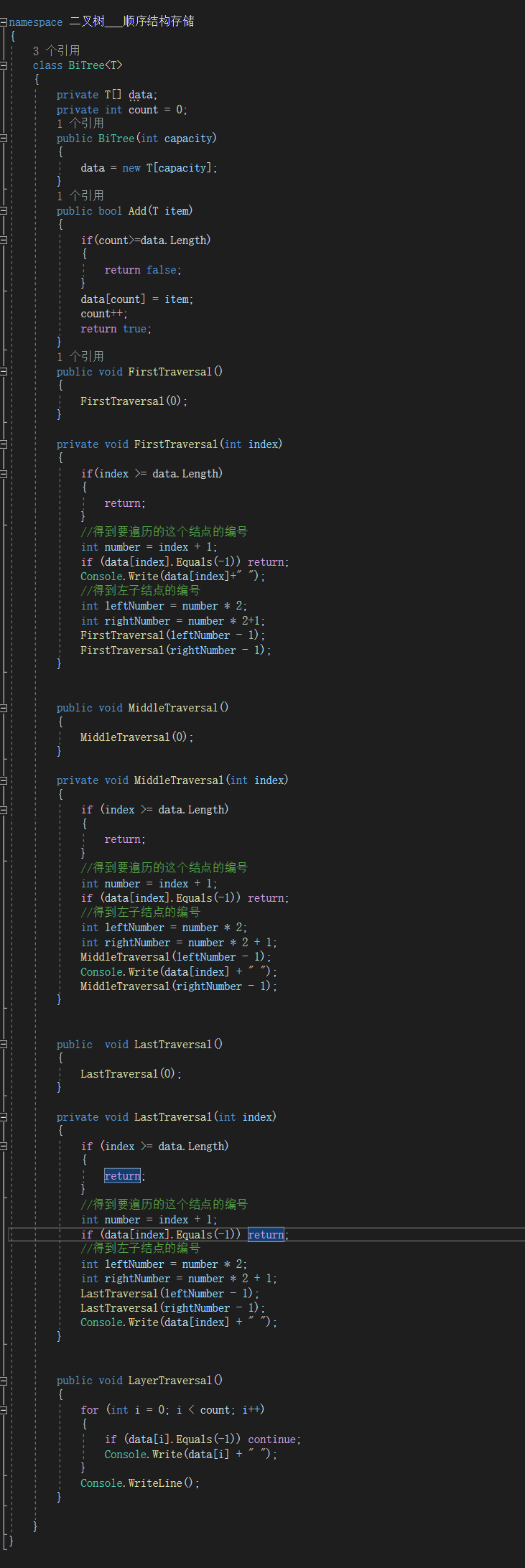
到此这篇关于c#二叉树存储介绍的文章就介绍到这了,更多相关c#二叉树存储内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!
相关推荐
-
C#非递归先序遍历二叉树实例
本文实例讲述了C#非递归先序遍历二叉树的方法.分享给大家供大家参考.具体如下: using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace ConsoleApplication5 { class Program { static void Main(string[] args) { Node treeRoo
-
关于c#二叉树的实现
本篇纯属娱乐,源于整理代码,发现还曾实现过遍历二叉树. 虽然.NET/C#中的各种集合类已经实现了最优的排序设计,但了解基本的算法实现有助于软件开发中的各种权衡和选择.比如,如果你实现过B+树排序和查找,并将树节点序列化至二进制文件块,则你应该已经了解了各种数据库索引的基本设计. 什么是二叉树?http://en.wikipedia.org/wiki/Binary_tree 二叉树节点类定义 复制代码 代码如下: View Code /// <summary> /// 二叉树节点
-
c#二叉树存储介绍
目录 存储结构 二叉树的遍历 存储结构 二叉树是一种特殊的树,给个结点最多有两个子节点,并且子节点有左右之分,并且兄弟,父亲,孩子可以很方便的通过编号得到 1.在二叉树的第i层上最多有2i-1个结点(i>=1) 2.深度为k的二叉树至多有2i-1个结点 3.对于一个二叉树,假设它有n个结点,对结点进行从1开始编号,对任一结点i满足下面 a.它的双亲是节点i/2(除了i=1的情况) b.左孩子是2i,右孩子是2i+1 c.如果2i>i说明无左孩子 2i+1>n说明无
-
Python实现基于二叉树存储结构的堆排序算法示例
本文实例讲述了Python实现基于二叉树存储结构的堆排序算法.分享给大家供大家参考,具体如下: 既然用Python实现了二叉树,当然要写点东西练练手. 网络上堆排序的教程很多,但是却几乎都是以数组存储的数,直接以下标访问元素,当然这样是完全没有问题的,实现简单,访问速度快,也容易理解. 但是以练手的角度来看,我还是写了一个二叉树存储结构的堆排序 其中最难的问题就是交换二叉树中两个节点. 因为一个节点最多与三个节点相连,那么两个节点互换,就需要考虑到5个节点之间的关系,也需要判断是左右孩子,这将是
-
JAVA二叉树的几种遍历(递归,非递归)实现
首先二叉树是树形结构的一种特殊类型,它符合树形结构的所有特点.本篇博客会针对二叉树来介绍一些树的基本概念,二叉树的基本操作(存储,返回树的深度,节点个数,每一层的节点个数),二叉树的四种遍历(层次,先序,中序,后序) 一.基本概念 二叉树有5种基本形态: 注:二叉树有序树,就是说一个节点的左右节点是有大小之分的,我们通常设定为左孩子一定大于右孩子,下面的实现都是基于这个规则的.二叉树分为三种:满二叉树,完全二叉树,不完全二叉树 二叉树的四种遍历:层次,先序,中序,后序首先是非递归实现上图的满二叉
-
C语言近万字为你讲透树与二叉树
目录 一.树概念及结构 1.1 树的概念 1.2 树的相关概念 1.3 树的表示 二.二叉树概念及结构 2.1 概念 2.2 特殊的二叉树: 2.3 二叉树的性质 2.4 二叉树的存储结构 1. 顺序存储 2. 链式存储 三.实现完全二叉树堆并实现堆排序 3.1 堆的概念和结构 3.2 实现堆的难点 3.3 小堆的实现 3.4 堆的应用-堆排序 四.Top-k问题 总结 一.树概念及结构 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合.把它叫
-
二叉树的概念案例详解
二叉树简介 关于树的介绍,请参考:https://blog.csdn.net/weixin_43790276/article/details/104033482 一.二叉树简介 二叉树是每个节点最多有两个子树的树结构,是一种特殊的树,如下图,就是一棵二叉树. 二叉树是由n(n>=0)个节点组成的数据集合.当 n=0 时,二叉树中没有节点,称为空二叉树.当 n=1 时,二叉树只有根节点一个节点.当 n>1 时,二叉树的每个节点都最多只能有两个子树,递归地构建成一棵完整的二叉树. 二叉树的两个子树
-
Python 二叉树的概念案例详解
二叉树简介 关于树的介绍,请参考:https://www.jb51.net/article/222488.htm 一.二叉树简介 二叉树是每个节点最多有两个子树的树结构,是一种特殊的树,如下图,就是一棵二叉树. 二叉树是由n(n>=0)个节点组成的数据集合.当 n=0 时,二叉树中没有节点,称为空二叉树.当 n=1 时,二叉树只有根节点一个节点.当 n>1 时,二叉树的每个节点都最多只能有两个子树,递归地构建成一棵完整的二叉树. 二叉树的两个子树被称为左子树(left subtree)和右子树
-
图文并茂地讲解Mysql索引(index)
目录 前言 1. 索引概述 1.1 什么是索引? 1.2 使用索引和不使用索引的区别 1.3 索引的特点 2. 索引结构 2.1 概述 2.2 二叉树 2.3 B-Tree 2.4 B+Tree 2.5 Hash 3.索引分类 3.1 索引分类 3.2 聚集索引&二级索引 4. 索引语法 5. SQL性能分析 5.1 SQL执行频率 5.2 慢查询日志 5.3 profile详情 5.4 explain 6. 索引使用 6.1 验证索引效率 6.2 最左前缀法则 6.3 索引失效情况 6.3.1
-
PHP脚本数据库功能详解(上)
在当前互联网发展迅速.电子商务网站层出不穷的形势下,对网站开发的效率和质量提出了越来越高的要求. 对于大型和结构复杂.内容繁多的网站,都要实现网站的动态化和方便的管理.数据管理离不开数据库系统的支持.而衡量一种CGI语言的重要标志,就是它对后台数据库的访问能力.效率等. 而目前流行的PHP脚本语言,它的新特性给我们带来了新的感觉.它支持以面向对象的方式进行设计开发.同时,为了满足网页独特的需要,用模板.XML支持等带来了网站开发的新方法.在语言结构上,PHP具有类似于C++语言的结构,并引入了类
-
Python编程二分法实现冒泡算法+快速排序代码示例
本文分享的实例主要是Python编程二分法实现冒泡算法+快速排序,具体如下. 冒泡算法: #-*- coding: UTF-8 -*- #冒泡排序 def func(lt): if type(lt).__name__ !='list' and type(lt).__name__ !='tuple': return if type(lt).__name__ == 'tuple': return list(lt) for i in range(1,len(lt)-1): for j in range
-
python实现堆和索引堆的代码示例
堆是一棵完全二叉树.堆分为大根堆和小根堆,大根堆是父节点大于左右子节点,并且左右子树也满足该性质的完全二叉树.小根堆相反.可以利用堆来实现优先队列. 由于是完全二叉树,所以可以使用数组来表示堆,索引从0开始[0:length-1].结点i的左右子节点分别为2i+1,2i+2.长度为length的树的最后一个非叶子节点为length//2-1.当前节点i的父节点为(i-1)//2.其中//表示向下取整. 以大根堆举例.当每次插入或者删除的时候,为了保证堆的结构特征不被破坏,需要进行调整.调整分为两
随机推荐
- Prototype使用指南之ajax
- JavaScript对象模型-执行模型
- splice slice区别
- java去除字符串中的空格、回车、换行符、制表符的小例子
- Python基于回溯法子集树模板解决最佳作业调度问题示例
- linux下mysql的root密码忘记的解决方法
- 创建无表格网站的原因和原则 译文
- 给blog加上运行代码功能
- SQL Server存储过程生成insert语句实例
- 超赞的jQuery图片滑块动画特效代码汇总
- 浅谈jQuery为哪般去掉了浏览器检测
- Android 系统net和wap接入点的区别
- Rxjava功能操作符的使用方法详解
- GOLANG使用Context实现传值、超时和取消的方法
- Python之循环结构
- Java开发之Lombok指南
- python 日期排序的实例代码
- node.js处理前端提交的GET请求
- java使用静态关键字实现单例模式
- CentOS6使用nginx搭建web网站服务的方法

