C#实现简单的二叉查找树

二叉查找树（Binary Search Tree），或者是一棵空树，或者是具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树。

二叉排序树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉排序树的存储结构。中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索,插入,删除的复杂度等于树高，O(log(n))。

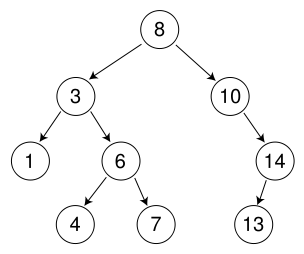
图 1. 三层二叉查找树

二叉排序树典型的用途是实现关联数组，一种常用的定义方式为：

class BiTree<TKey,TValue> where TKey:IComparable
{
    public TKey Key { get; set; }
    public TValue Value { get; set; }

    BiTree<TKey, TValue> Left { get; set; }
    BiTree<TKey, TValue> Right { get; set; }

    public BiTree(TKey key,TValue value)
    {
        this.Key = key;
        this.Value = value;
    }
}

二叉排序树的查找算法

在二叉排序树b中查找x的过程为：

• 若b是空树，则搜索失败，否则：
• 若x等于b的根结点的数据域之值，则查找成功；否则：
• 若x小于b的根结点的数据域之值，则搜索左子树；否则：
• 查找右子树。

public TValue Search(TKey key)
{
    int ret = key.CompareTo(this.Key);

    if (ret == 0)
    {
        return Value;
    }
    else
    {
        var subTree = ret < 0 ? Left : Right;
        if (subTree == null)
        {
            throw new KeyNotFoundException();
        }
        else
        {
            return subTree.Search(key);
        }
    }
}

在二叉排序树插入结点的算法

一种简单的向一个二叉排序树b中插入一个结点s的算法为：

• 若b是空树，则将s所指结点作为根结点插入，否则：
• 若s->data等于b的根结点的数据域之值，则返回，否则：
• 若s->data小于b的根结点的数据域之值，则把s所指结点插入到左子树中，否则：
• 把s所指结点插入到右子树中。

public void Insert(TKey key, TValue value)
{
    int ret = key.CompareTo(this.Key);

    if (ret == 0)
    {
        this.Value = value;
    }
    else
    {
        var subTree = ret < 0 ? Left : Right;
        if (subTree == null)
        {
            subTree = new BiTree<TKey, TValue>(key, value);
            if (ret < 0)
                Left = subTree;
            else
                Right = subTree;
        }
        else
        {
            subTree.Insert(key, value);
        }
    }
}

在二叉排序树删除结点的算法

在二叉排序树删去一个结点，分三种情况讨论：

• 若*p结点为叶子结点，即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构，则只需修改其双亲结点的指针即可。
• 若*p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点*f的左子树即可，作此修改也不破坏二叉排序树的特性。
• 若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整，可以有两种做法：其一是令*p的左子树为*f的左子树，*s为*f左子树的最右下的结点，而*p的右子树为*s的右子树；其二是令*p的直接前驱（或直接后继）替代*p，然后再从二叉排序树中删去它的直接前驱（或直接后继）。

二叉排序树性的遍历

二叉排序树一般采用先根访问，这样能将所有元素按大小排序访问。

public void Visit(Action<TKey, TValue> visitor)
{
    if (Left != null)
    {
        Left.Visit(visitor);
    }

    visitor(Key, Value);

    if (Right != null)
    {
        Right.Visit(visitor);
    }
}

二叉排序树性能分析

每个结点的Ci为该结点的层次数。最坏情况下，当先后插入的关键字有序时，构成的二叉排序树蜕变为单支树，树的深度为n，其平均查找长度为

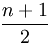
（和顺序查找相同），最好的情况是二叉排序树的形态和折半查找的判定树相同，其平均查找长度和log2(n)成正比（O(log2(n))）。

到此这篇关于C#实现二叉查找树的文章就介绍到这了。希望对大家的学习有所帮助，也希望大家多多支持我们。