Java二叉树查询原理深入分析讲解

目录

• 二叉查询树
• 结点实现原理
• 插入实现原理
• 遍历实现原理
• 删除实现原理
• 结点插入与遍历案例

二叉查询树

概述

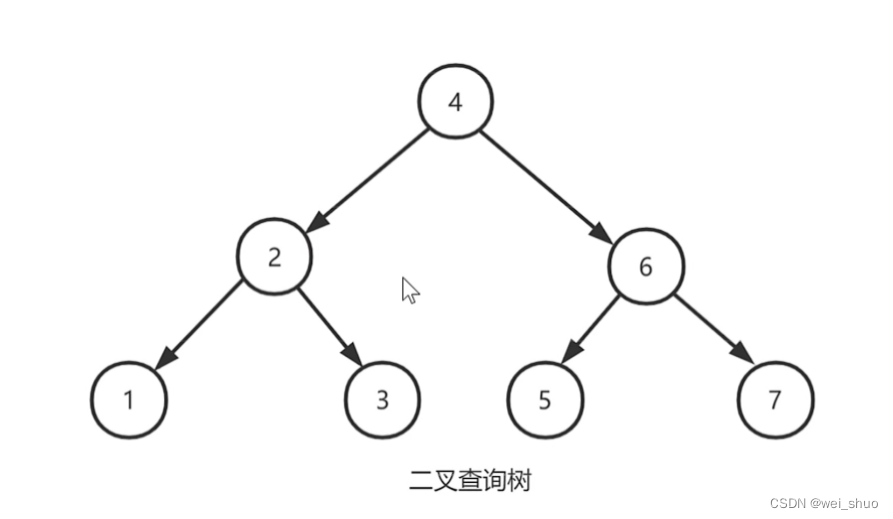
二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分

特点

树同时具有数组查询的效率、链表增删、改的性能

右子树的结点比左子树的节点大

查找法

搜索的数字如果比节点大则往右搜索，搜索的数字如果比节点小则往左搜索

结点实现原理

插入实现原理

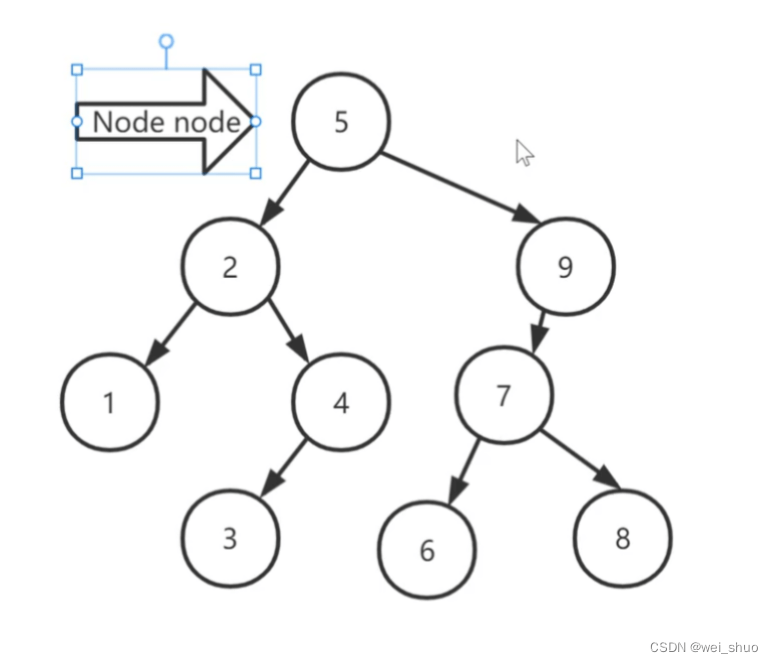
int[] arrs = {5,2,1,4,3,9,7,6,8};

如果树是空树，插入节点就直接放入到根结点

如果树不是空树，则插入的数字于根结点的数字进行比较

如果插入的值小于于结点的数字，则往左子树插入

• 如果左子结点没有元素就插入到左子结点中
• 如果左子结点有元素，就可以设计一个引用(游标)指向左子节点，并且再次和待插入的执行左子结点进行比较，直到找到插入的位置

如果插入的值大于结点的数字，则往右子树插入

• 判断右子结点是否存在值，如果不存在则直接插入
• 判断右子结点是否存在值，如果存在则通过一个引用指向右子结点继续和待插入的值进行比较，直到找到插入的位置

总结：

• 小往左，大往右
• 左子数永远小于右子树

遍历实现原理

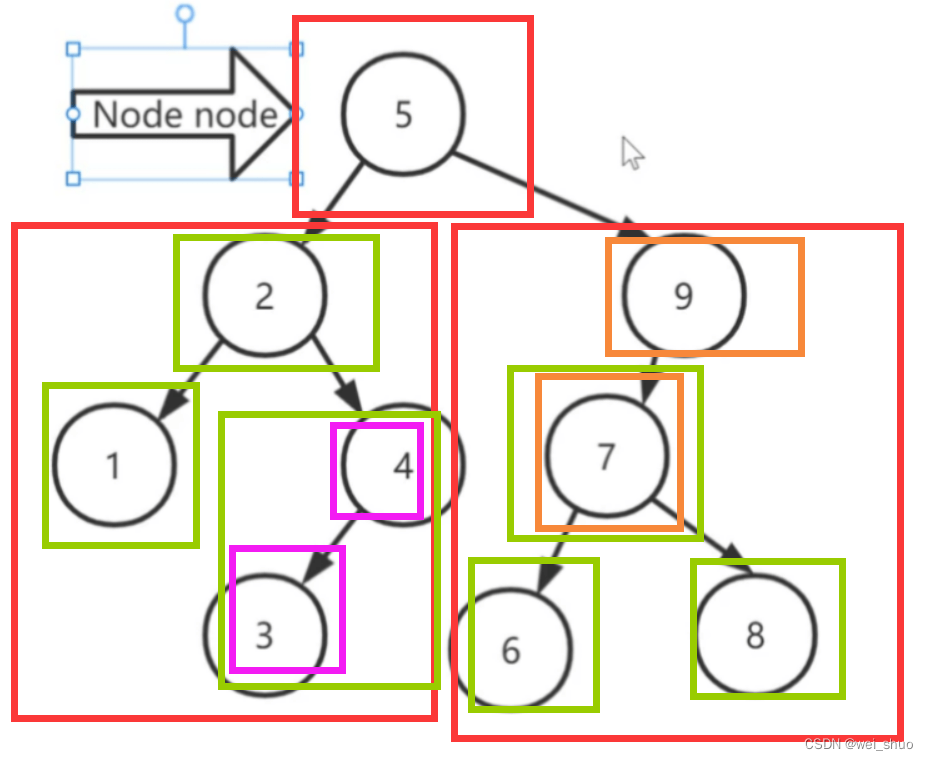
中序遍历：左—根—右

通过中序遍历就可以将二叉树查找树的进行顺序输出

总结：

始终贯彻左—根—右的原则、由内层向外层拆分

int[] arrs = {1,2,3,4,5,6,7,8,9};

删除实现原理

提供一个待删除的结点的值，根据值从二叉查找树找到需要删除的结点

找到待删除结点的父类结点，并且要根据待删除结点在父类结点的左右子树的位置，设置为null进行删除

需要考虑结点的三种情况

情况1：待删除的结点没有子结点

直接让父类结点的对应目标结点引用设置为null即可

情况2：待删除的结点有一个子节点

将待删除的父类结点对应子节点的引用指向待删除结点的子节点

情况3：待删除的结点有两个子节点 从左子树中找到最大的结点进行删除，并且将最大的结点的值放入到待删除结点从右子树中找到最小的结点进行删除，并且将最小的结点的值放入(替换)到待删除结点

(上述两种删除方法：需要将待删除结点指向新创建(替换后的)的结点，并且将新的结点(替换后的)的左右结点指向待删除的左右子树的结点)

删除的结点是根节点的情况

情况1：根节点没有子节点，直接将根结点指向null

情况2：根结点有一个子节点，则根结点直接指向子节点

情况3：根结点有两个子节点

可以从左子树中找到最大值删除结点，然后将最大值覆盖(替换)根节点

可以从右子树中找到最小值删除结点，然后将最小值覆盖(替换)根节点

结点插入与遍历案例

BinarySearchTree类

package Algorithm;
public class BinarySearchTree {
    Node root;  //定义根节点
    //结点插入方法
    public void insert(int value) {
        if (root == null) {        //1.如果树是空树，插入节点就直接放入到根结点
            root = new Node(value);
        } else {     //如果树不是空树，则插入的数字于根结点的数字进行比较
            //2.如果插入的值小于于结点的数字，则往左子树插入
            Node node = root;     //声明一个游标结点，开始指向根节点
            while (true) {       //并且再次和待插入的执行左子结点进行比较，直到找到插入的位置
                if (value < node.value) {      //如果插入的值小于于结点的数字，则往左子树插入
                    //2.1如果左子结点没有元素就插入到左子结点中
                    if (node.left == null) {
                        node.left = new Node(value);
                        break;      //如果找到插入的位置，则跳出while循环
                    } else {         //如果左子结点有元素，就可以设计一个引用(游标)指向左子节点，并且再次和待插入的执行左子结点进行比较，直到找到插入的位置
                        //游标指向左子节点
                        node = node.left;
                    }
                } else {      //如果插入的值大于结点的数字，则往右子树插入
                    //判断右子结点是否存在值，如果不存在则直接插入
                    if (node.right == null) {
                        node.right = new Node(value);
                        break;
                    } else {     //判断右子结点是否存在值，如果存在则通过一个引用指向右子结点继续和待插入的值进行比较，直到找到插入的位置
                        //游标指向右子节点
                        node = node.right;
                    }
                }
            }
        }
    }
    //定义左右结点常量
    public static final int LEFT = 0; //左子节点
    public static final int RIGHT = 1; //右子节点
    //结点查找方法
    public void deleteNode(int value) {
        //定义游标从根节点开始查询
        Node node = root;
        //定义目标结点
        Node target = null;
        //定义目标结点的父类结点
        Node parent = null;
        //目标结点的类型为，左子节点或者右子节点
        int nodeType = 0; //0代表左子节点 1代表右子节点

        while (node != null) { //游标不为空，如果为空则没有子节点，无法删除
            if (node.value == value) { //如果目标结点的值和需要删除结点的值相同
                //找到结点
                target = node;
                break;
            } else if (value < node.value) {    //如果值不同，则判断目标结点值是否小于node结点
                //保存父类结点
                parent = node;
                //游标指向左子节点
                node = node.left;
                nodeType = LEFT;
            } else { //如果值不同，且目标结点值大于node结点
                //保存父类结点
                parent = node;
                //游标指向右子节点
                node = node.right;
                nodeType = RIGHT;
            }
        }
        //如果没找到需要删除的目标结点
        if (target==null){
            System.out.println("没有找到要删除的结点");
            return;
        }
        //删除结点的三种情况
        if (target.left == null && target.right == null) {   //情况1：待删除的结点没有子结点

            if (parent==null){      //删除的结点没有子结点
                //将root设置为null即可
                root=null;
                return;
            }
            //判断目标的结点是左子节点还是右子节点
            if (nodeType == LEFT) {
                //将父类的左子节点设置为null
                parent.left = null;
            } else {
                //将父类的右子节点设置为null
                parent.right = null;
            }
        } else if (target.left != null && target.right != null) {   //情况2：待删除的结点有2个子节点
            //两个子节点，从target右子树查找最小的值
            Node min=target.right;
            //遍历左子树
            while (min.left!=null){
                min = min.left;
            }
            //将最小的结点进行删除
            deleteNode(min.value);
            //将待删除的结点替换成最小的结点的值
            target.value= min.value;
        }else { //情况3：待删除的结点有1个子节点
            //删除结点是根节点
            if (parent==null){
                if (target.left!=null){ //判断是左子节点还是右子节点有值
                    root=target.left;   //根节点=目标左子结点
                }else {
                    root=target.right;  //根节点=目标右子结点
                }
            }
            //只有一个子节点
            if (nodeType==LEFT){    //如果是左子节点
                if (target.left!=null){
                    //将父类的左子节点，指向待删除结点的左子节点
                    parent.left=target.left;
                }else { //如果是右子节点
                    //将父类的左子节点，指向待删除结点的右子节点
                    parent.left=target.right;
                }
            }else {
                if (target.right!=null){
                    //将父类的右子节点，指向待删除结点的左子节点
                    parent.right=target.left;
                }else { //如果是右子节点
                    //将父类的右子节点，指向待删除结点的右子节点
                    parent.right=target.right;
                }
            }
        }
    }
    //实现中序遍历
    public void midTraversal(Node node) {
        if (node == null) {  //进行判断结点不能为空，如果为空则退出
            return;
        } else {     //如果结点不为null，则执行下列遍历语句
            //首先，遍历左节点
            midTraversal(node.left);
            //打印根节点
            System.out.print(node.value + ",");
            //最后遍历右子结点
            midTraversal(node.right);
        }
    }
    //创建一个结点类
    public static class Node {
        int value;  //存储值
        Node left;  //左子树
        Node right; //右子树
        // 带参构造方法，传入value赋值
        public Node(int value) {
            this.value = value;
        }
    }
}

TestBST测试类

package Algorithm;
public class TestBST {
    public static void main(String[] args) {
        int[] arrs = {5, 2, 1, 4, 3, 9, 7, 6, 8};
        //创建二叉查询树
        BinarySearchTree tree = new BinarySearchTree();
        //将数组中的元素构造成二叉查询树
        for (int i = 0; i < arrs.length; i++) {
            tree.insert(arrs[i]);
        }
        //删除结点
        tree.deleteNode(20);
        //中序遍历根结点
        tree.midTraversal(tree.root);
    }
}

到此这篇关于Java二叉树查询原理深入分析讲解的文章就介绍到这了,更多相关Java二叉树查询内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！