torch.optim优化算法理解之optim.Adam()解读

目录

• optim.Adam()解读
• 优化步骤
• Adam算法
• 其公式如下
• 参数
• torch.optim.adam源码
• Adam的特点有

optim.Adam()解读

torch.optim是一个实现了多种优化算法的包，大多数通用的方法都已支持，提供了丰富的接口调用，未来更多精炼的优化算法也将整合进来。

为了使用torch.optim，需先构造一个优化器对象Optimizer，用来保存当前的状态，并能够根据计算得到的梯度来更新参数。

要构建一个优化器optimizer，你必须给它一个可进行迭代优化的包含了所有参数（所有的参数必须是变量s）的列表。 然后，您可以指定程序优化特定的选项，例如学习速率，权重衰减等。

optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)
optimizer = optim.Adam([var1, var2], lr = 0.0001)
self.optimizer_D_B = torch.optim.Adam(self.netD_B.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

• Optimizer还支持指定每个参数选项。 只需传递一个可迭代的dict来替换先前可迭代的Variable。
• dict中的每一项都可以定义为一个单独的参数组，参数组用一个params键来包含属于它的参数列表。

其他键应该与优化器接受的关键字参数相匹配，才能用作此组的优化选项。

optim.SGD([
                {'params': model.base.parameters()},
                {'params': model.classifier.parameters(), 'lr': 1e-3}
            ], lr=1e-2, momentum=0.9)

如上，model.base.parameters()将使用1e-2的学习率，model.classifier.parameters()将使用1e-3的学习率。0.9的momentum作用于所有的parameters。

优化步骤

所有的优化器Optimizer都实现了step()方法来对所有的参数进行更新，它有两种调用方法：

optimizer.step()

这是大多数优化器都支持的简化版本，使用如下的backward()方法来计算梯度的时候会调用它。

for input, target in dataset:
    optimizer.zero_grad()
    output = model(input)
    loss = loss_fn(output, target)
    loss.backward()
    optimizer.step()

optimizer.step(closure)

一些优化算法，如共轭梯度和LBFGS需要重新评估目标函数多次，所以你必须传递一个closure以重新计算模型。 closure必须清除梯度，计算并返回损失。

for input, target in dataset:
    def closure():
        optimizer.zero_grad()
        output = model(input)
        loss = loss_fn(output, target)
        loss.backward()
        return loss
    optimizer.step(closure)

Adam算法

adam算法来源：Adam: A Method for Stochastic Optimization

Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。它的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。

其公式如下

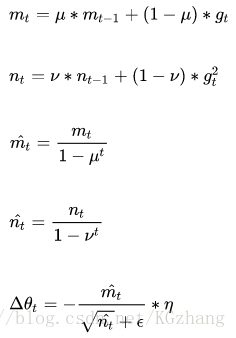
其中，前两个公式分别是对梯度的一阶矩估计和二阶矩估计，可以看作是对期望E|gt|，E|gt^2|的估计;

公式3，4是对一阶二阶矩估计的校正，这样可以近似为对期望的无偏估计。可以看出，直接对梯度的矩估计对内存没有额外的要求，而且可以根据梯度进行动态调整。

最后一项前面部分是对学习率n形成的一个动态约束，而且有明确的范围。

class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)

参数

• params(iterable)：可用于迭代优化的参数或者定义参数组的dicts。
• lr (float, optional) ：学习率(默认: 1e-3)
• betas (Tuple[float, float], optional)：用于计算梯度的平均和平方的系数(默认: (0.9, 0.999))
• eps (float, optional)：为了提高数值稳定性而添加到分母的一个项(默认: 1e-8)
• weight_decay (float, optional)：权重衰减(如L2惩罚)(默认: 0)
• step(closure=None)函数：执行单一的优化步骤
• closure (callable, optional)：用于重新评估模型并返回损失的一个闭包

torch.optim.adam源码

import math
from .optimizer import Optimizer

class Adam(Optimizer):
    def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8，weight_decay=0):
        defaults = dict(lr=lr, betas=betas, eps=eps,weight_decay=weight_decay)
        super(Adam, self).__init__(params, defaults)

    def step(self, closure=None):
        loss = None
        if closure is not None:
            loss = closure()

        for group in self.param_groups:
            for p in group['params']:
                if p.grad is None:
                    continue
                grad = p.grad.data
                state = self.state[p]

                # State initialization
                if len(state) == 0:
                    state['step'] = 0
                    # Exponential moving average of gradient values
                    state['exp_avg'] = grad.new().resize_as_(grad).zero_()
                    # Exponential moving average of squared gradient values
                    state['exp_avg_sq'] = grad.new().resize_as_(grad).zero_()

                exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
                beta1, beta2 = group['betas']

                state['step'] += 1

                if group['weight_decay'] != 0:
                    grad = grad.add(group['weight_decay'], p.data)

                # Decay the first and second moment running average coefficient
                exp_avg.mul_(beta1).add_(1 - beta1, grad)
                exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)

                denom = exp_avg_sq.sqrt().add_(group['eps'])

                bias_correction1 = 1 - beta1 ** state['step']
                bias_correction2 = 1 - beta2 ** state['step']
                step_size = group['lr'] * math.sqrt(bias_correction2) / bias_correction1

                p.data.addcdiv_(-step_size, exp_avg, denom)

        return loss

Adam的特点有

1、结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点;

2、对内存需求较小;

3、为不同的参数计算不同的自适应学习率;

4、也适用于大多非凸优化-适用于大数据集和高维空间。

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。