FP-growth算法发现频繁项集——发现频繁项集

上篇介绍了如何构建FP树，FP树的每条路径都满足最小支持度，我们需要做的是在一条路径上寻找到更多的关联关系。

抽取条件模式基

　　首先从FP树头指针表中的单个频繁元素项开始。对于每一个元素项，获得其对应的条件模式基（conditional pattern base)，单个元素项的条件模式基也就是元素项的关键字。条件模式基是以所查找元素项为结尾的路径集合。每一条路径其实都是一条前辍路径（perfix path）。简而言之，一条前缀路径是介于所査找元素项与树根节点之间的所有内容。

　　下图是以{s:2}或{r:1}为元素项的前缀路径：

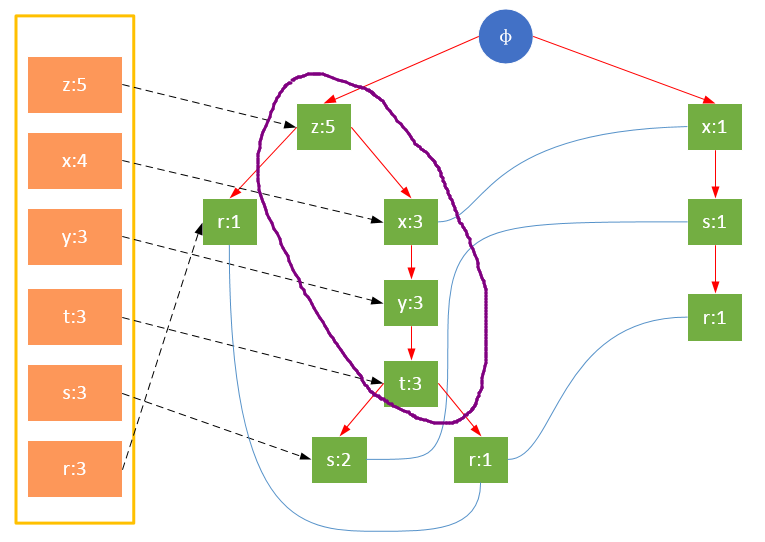
　　{s}的条件模式基，即前缀路径集合共有两个：{{z,x,y,t}, {x}}；{r}的条件模式基共三个：{{z}, {z,x,y,t}, {x,s}}。

　　寻找条件模式基的过程实际上是从FP树的每个叶子节点回溯到根节点的过程。我们可以通过头指针列表headTable开始，通过指针的连接快速访问到所有根节点。下表是上图FP树的所有条件模式基：

创建条件FP树

　　为了发现更多的频繁项集，对于每一个频繁项，都要创建一棵条件FP树。可以使用刚才发现的条件模式基作为输入数据，并通过相同的建树代码来构建这些树。然后，递归地发现频繁项、发现条件模式基，以及发现另外的条件树。

　　以频繁项r为例，构建关于r的条件FP树。r的三个前缀路径分别是{z},{z,x,y,t},{x,s}，设最小支持度minSupport=2，则y,t,s被过滤掉，剩下{z},{z,x},{x}。y,s,t虽然是条件模式基的一部分，但是并不属于条件FP树，即对于r来说，它们不是频繁的。如下图所示，y→t→r和s→r的全局支持度都为1，所以y,t,s对于r的条件树来说是不频繁的。

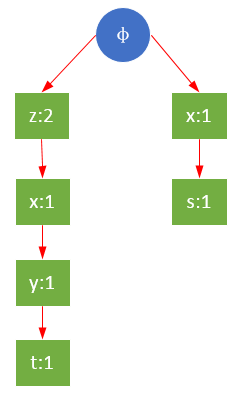
　　过滤后的r条件树如下：

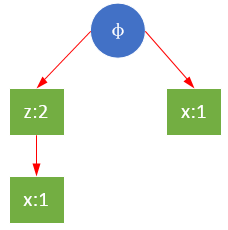
　　重复上面步骤，r的条件模式基是{z,x},{x}，已经没有能够满足最小支持度的路径， 所以r的条件树仅有一个。需要注意的是，虽然{z,x},{x}中共存在两个x，但{z,x}中，z是x的父节点，在构造条件FP树时不能直接将父节点移除，仅能从子节点开始逐级移除。

　　代码如下：

def ascendTree(leafNode, prefixPath):
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)
def findPrefixPath(basePat, headTable):
    condPats = {}
    treeNode = headTable[basePat][1]
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink
    return condPats
def mineTree(inTree, headerTable, minSup=1, preFix=set([]), freqItemList=[]):
    # order by minSup asc, value asc
    bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: (p[1][0],p[0]))]
    for basePat in bigL:
        newFreqSet = preFix.copy()
        newFreqSet.add(basePat)
        freqItemList.append(newFreqSet)
        # 通过条件模式基找到的频繁项集
        condPattBases = findPrefixPath(basePat, headerTable)
        myCondTree, myHead = createTree(condPattBases, minSup)
        if myHead != None:
            print('condPattBases: ', basePat, condPattBases)
            myCondTree.disp()
            print('*' * 30)
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
simpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
condPats = findPrefixPath('z', myheader)
print('z', condPats)
condPats = findPrefixPath('x', myheader)
print('x', condPats)
condPats = findPrefixPath('y', myheader)
print('y', condPats)
condPats = findPrefixPath('t', myheader)
print('t', condPats)
condPats = findPrefixPath('s', myheader)
print('s', condPats)
condPats = findPrefixPath('r', myheader)
print('r', condPats)
mineTree(myFPTree, myheader, 2)

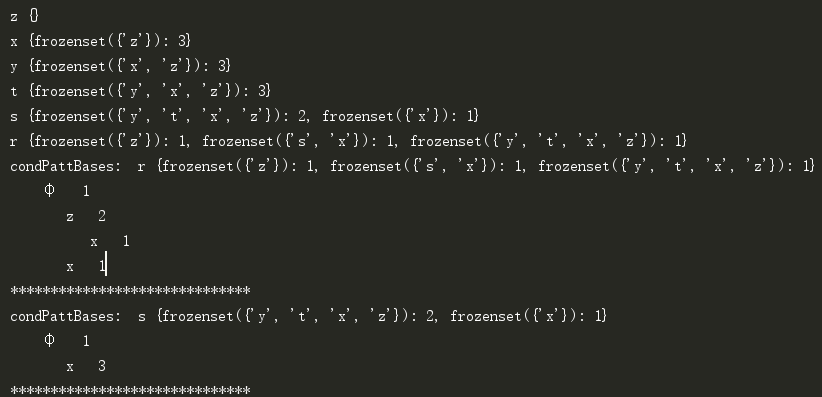
　　控制台信息：

总结

本篇文章就到这了，本例可以发现两个频繁项集{z,x}和{x}。取得频繁项集后，可以根据置信度发现关联规则，这一步较为简单，可参考上篇的相关内容，不在赘述。希望能够给你带来帮助，也希望您能够多多关注我们的其他精彩内容！