归并排序时间复杂度过程推导详解

目录
  • 归并排序
  • 总结

归并排序

归并排序方法就是把一组n个数的序列，折半分为两个序列，然后再将这两个序列再分，一直分下去，直到分为n个长度为1的序列。然后两两按大小归并。如此反复，直到最后形成包含n个数的一个数组。

归并排序总时间=分解时间+子序列排好序时间+合并时间

无论每个序列有多少数都是折中分解，所以分解时间是个常数，可以忽略不计。

则：归并排序总时间=子序列排好序时间+合并时间

如果假设一个序列有n个数的排序时间为T(n)，T(n)是一个关于n的函数，随着n的变化而变化。

那么我们将n个数的序列，分为两个(n/2)的序列。

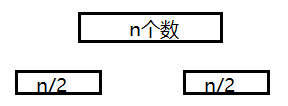
那么T(n)=2*T(n/2)+合并时间

由于合并时，两个子序列已经组内排好序了，那我们将两个排好序的序列组合成一个大的有序序列，只需要一个if循环即可。if循环中有n个数需要比较，所以时间复杂度为n。

那么T(n)=2*T(n/2)+n

我们再将两个n/2个序列再分成4个(n/4)的序列。

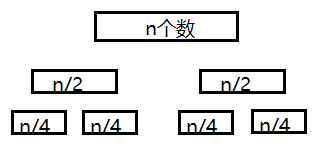
一个（n/2）序列排序时间=两个(n/4)的序列排序时间+两个(n/4)的序列的合并为一个（n/2）的序列时间

T(n/2)=2*T(n/4)+n/2

将T(n/2)带入到T(n)中，T(n)=2*(2*T(n/4)+n/2)+n，

通过化简T(n)=4*T(n/4)+2n

我们再将4个n/4个序列再分成8个(n/8)的序列。

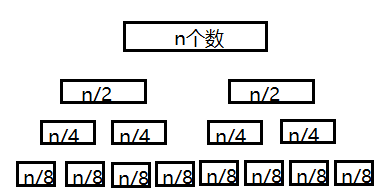
T(n/4)=2*T(n/8)+n/4

将T(n/4)带入到黄色公式中，T(n)=4*(2*T(n/8)+n/4)+2n

通过化简T(n)=8*T(n/8)+3n

这样分下去，前面我们已经说过了，分为n个序列，每个序列里只有一个数为止。

前面我们假设的一个序列有n个数的排序时间为T(n)，现在每个序列只有一个数，所以不需要进行组内排序，时间复杂度为0。T(1)=0

大家有没有找到规律，右边式子中n前面的系数随着层数的增加而增加，第一层公式中没有n，则系数为0，第二层n的系数为1，第三层为2，第四层为3。那么规律就出来了，n前面的系数为层数减1。

那这个图有没有很熟悉，就像一个二叉树一样，通过二叉树的知识点我们可以知道，一个n个结点的完全二叉树层数为(log2n)+1。

那么n前面的系数为层数减1。

(log2n)+1-1=log2n

那log2n就是最底层n的系数。

那么我们最后一层是不是可以这样表示

T(n)=n*T(1)+(log2n)*n

T(1)=0，那么T(n)=(log2n)*n

所以归并排序的时间复杂度为nlog2n

总结

本篇文章就到这里了，希望能给你带来帮助，也希望您能够多多关注我们的更多内容！

赞 (0)

相关推荐

  • Java排序算法三之归并排序的递归与非递归的实现示例解析

    归并有递归和非递归两种. 归并的思想是: 1.将原数组首先进行两个元素为一组的排序,然后合并为四个一组,八个一组,直至合并整个数组: 2.合并两个子数组的时候,需要借助一个临时数组,用来存放当前的归并后的两个数组: 3.将临时数组复制回原数组对应的位置. 非递归的代码如下: package mergesort; import java.util.Arrays; import java.util.Random; import java.util.Scanner; //归并排序的非递归算法 publ

  • C++实现归并排序（MergeSort）

    本文实例为大家分享了C++实现归并排序的具体代码,供大家参考,具体内容如下 一.思路:稳定排序 (1)划分:一直调用划分过程,直到子序列为空或只有一个元素为止,共需log2(n): (2)归并:将两个子序列从小到大合并为一个序列 二.实现程序: // 归并排序:(二路归并) // (1)递归分解数组: // (2)合并有序的序列 #include <iostream> using namespace std; // 合并两个有序的序列 template <typename T> v

  • python基本算法之实现归并排序(Merge sort)

    0.前言 评判一个算法的好坏的标准: 时间复杂度 空间复杂度 1.归并排序算法是什么? 冒泡排序(Bubble Sort)是一种建立在归并操作上面的一种有效的排序算法,由John von neumann于1945年发明.采用分治法(Divide and Conquer)的经典应用!!将规模较大的排序问题化归到较小的规模上解决. 基本实现包含下面的两种方法: 自上而下的递归 自下而上的迭代 将已经有的有序子序列合并,得到完全有序的子序列.就是先得到每个子序列有序,然后在使得两个子序列合并成为一个有

  • Java 利用递归实现链表的归并排序

    利用归并排序,我们可以将时间复杂度降至O(nlogn), 并且我们是对链表进行排序,可以通过修改引用来更改节点顺序,无需像数组一样开辟而外的空间. 利用递归实现链表的归并排序有两个环节: 分割cut环节: 我们可以利用fast, slow快慢双指针实现链表的分割, fast一次移动两位, slow一次移动一位,当fast移动到末尾时,slow移动到中间位置. 利用变量为tmp = slow.next记录后链表的头节点,并将slow.next = null将前后链表断开. ListNode sor

  • python归并排序算法过程实例讲解

    关于python的算法一直都是让我们又爱又恨,但是如果可以灵活运用起来,对我们的编写代码过程,可以大大提高效率,针对算法之一"归并排序"的灵活掌握,一起来看下吧~ 归并算法--小试牛刀 实例内容: 有 1 个无序列表如下: list = [23,35,12,34,54,78,76,99] 要求:使其按从小到大排序 图示思路 Python 代码 归并排序理解: 1.通过二分法把一个数组按照递归拆分为左右两组(至到独立元素为止) 2.按照从底层往高层的方法左右数组对比,同时对两个数组的第一

  • 归并排序时间复杂度过程推导详解

    归并排序时间复杂度过程推导详解

    目录 归并排序 总结 归并排序 归并排序方法就是把一组n个数的序列,折半分为两个序列,然后再将这两个序列再分,一直分下去,直到分为n个长度为1的序列.然后两两按大小归并.如此反复,直到最后形成包含n个数的一个数组. 归并排序总时间=分解时间+子序列排好序时间+合并时间 无论每个序列有多少数都是折中分解,所以分解时间是个常数,可以忽略不计. 则:归并排序总时间=子序列排好序时间+合并时间 如果假设一个序列有n个数的排序时间为T(n),T(n)是一个关于n的函数,随着n的变化而变化. 那么我们将n个

  • Java 数据结构之时间复杂度与空间复杂度详解

    Java 数据结构之时间复杂度与空间复杂度详解

    目录 算法效率 时间复杂度 什么是时间复杂度 推导大 O 阶的方法 算法情况 计算冒泡排序的时间复杂度 计算二分查找的时间复杂度 计算阶乘递归的时间复杂度 计算斐波那契递归的时间复杂度 空间复杂度 计算冒泡排序的空间复杂度 计算斐波那契数列的空间复杂度(非递归) 计算阶乘递归Factorial的时间复杂度 算法效率 在使用当中,算法效率分为两种,一是时间效率(时间复杂度),二是空间效率(空间复杂度).时间复杂度是指程序运行的速度.空间复杂度是指一个算法所需要的额外的空间. 时间复杂度 什么是时间

  • java中归并排序和Master公式详解

    java中归并排序和Master公式详解

    目录 基本思想 实现 对数器验证 递归时间复杂度计算 Master 公式 总结 基本思想 归并排序采取分治的思想进行排序,借用一张图片说明一下 将n个元素从中间切开,分成两部分.(左边可能比右边多1个数) 将步骤1分成的两部分,再分别进行递归分解.直到所有部分的元素个数都为1. 从最底层开始逐步合并两个排好序的数列.优点在于,分治之后,合并排序的过程时间复杂度是O(N)(只需要扫描一遍就可以将两个有序的数组合并成一个有序数组) 实现 public static void MergeSort(in

  • MySQL5.7.18下载和安装过程图文详解

    MySQL5.7.18下载和安装过程图文详解

    MySql下载 1.打开官网找到下载路口,这里直接给出下载的地址 https://dev.mysql.com/downloads/mysql/ 2.选择64位版本 3.直接下载  MySql5.7.18.1安装过程 1   .运行安装软件,接受协议 2.选择默认安装 3.下一步到检查环境界面,点击"Execute"执行检查 (可以后面单独下载插件安装),点击Next 4.点击"Execute"安装产品,安装成功后会打钩,然后Next 5.点击Next进入配置 6.默

  • win7-vs2012下安装.net frame work 的过程图文详解

    第一, vs和.net的对应关系大致如下 vs2010----.net framework 4.0 vs2012----.net framework 4.5 vs2015----.net framework 4.6.1 vs2017----.net framework 4.6.2 第二,在win7上安装vs2010之后会有.net4.5 frame work已经安装好了. vs2012 update5 也可以安装,但不是必须的. 第三,如果以后的开发不需要用到4.5.1 4.5.2 4.6 4.

  • Python程序包的构建和发布过程示例详解

    关于我 编程界的一名小程序猿,目前在一个创业团队任team lead,技术栈涉及Android.Python.Java和Go,这个也是我们团队的主要技术栈. 联系:hylinux1024@gmail.com 当我们开发了一个开源项目时,就希望把这个项目打包然后发布到 pypi.org 上,别人就可以通过 pip install 的命令进行安装.本文的教程来自于 Python 官方文档 , 如有不正确的地方欢迎评论拍砖. 0x00 创建项目 本文使用到的项目目录为 ➜ packaging-tuto

  • Hadoop-3.1.2完全分布式环境搭建过程图文详解（Windows 10）

    一.前言 Hadoop原理架构本人就不在此赘述了,可以自行百度,本文仅介绍Hadoop-3.1.2完全分布式环境搭建(本人使用三个虚拟机搭建). 首先,步骤: ① 准备安装包和工具: hadoop-3.1.2.tar.gz ◦ jdk-8u221-linux-x64.tar.gz(Linux环境下的JDK) ◦ CertOS-7-x86_64-DVD-1810.iso(CentOS镜像) ◦工具:WinSCP(用于上传文件到虚拟机),SecureCRTP ortable(用于操作虚拟机,可复制粘

  • MySQL5.7.24版本的数据库安装过程图文详解

    MySQL 是最流行的关系型数据库管理系统,在WEB应用方面 MySQL 是最好的RDBMS(Relational Database Management System:关系数据库管理系统)应用软件之一. 一:MySQL安装包下载 打开网站去下载MySQL(MySQL下载地址链接) 这个网站链接进去是默认的最新版本的MySQL,所以假如需要下载5.7版本的,需要点击下面图上的链接进行下载. 选择对应你电脑的版本,现在一般都是64位的电脑. 接下来,点击Download,选择No thanks,

  • 在idea中将创建的java web项目部署到Tomcat中的过程图文详解

    在idea中将创建的java web项目部署到Tomcat中 采用的工具idea 2018.3.6 Tomcat7 1.先创建第一个新项目secondweb(注意勾选JavaEE下的web Application(4.0),窗口下的version对应为4.0,并且保证create web.xml已经被勾选) 2.在创建好的web项目的web/WEB-INF目录下创建两个文件夹:classes和lib.classes用来存放编译后输出的class文件,lib用来存放第三方jar包(下图显示的是创建

  • IDEA插件开发之环境搭建过程图文详解

    基于IntelliJ Platform Plugin搭建 环境步骤 File->New->Project 选择IntelliJ Platform Plugin 如果你这里没有SDK环境,则添加一个SDK环境,选择自己的idea的安装的根目录即可. 展示效果 基于Gradle搭建环境步骤 File->New->Project 选择Gradle next 进来以后大概是这样的一个界面,然后gradle会自动build项目,下载相关的依赖.(可能会失败) 遇到的问题一,依赖ideaIC-

随机推荐