c++实现单纯形法现行规划问题的求解(推荐)

在本程序中默认该现行规划问题有最优解

针对此问题：

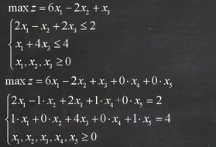
#include<iostream>
using namespace std;

int check(float *sigema, int m) {
  for (int i = 1; i <= m ; i++) {
    if (sigema[i] > 0) {
      return 0;
    }
  }
  return 1;
}

//此程序已经化为标准型的线性规划问题中,且默认有最优解
int main(int argc, char* argv[])
{
  //数据输入部分
  int m, n;
  cout << "请输入变量个数：";
  cin >> m;
  cout << "请输入不等式个数:";
  cin >> n;
  float **matrix = new float*[n + 1];   //系数矩阵
  for (int i = 1; i <= n; i++) {
    matrix[i] = new float[m + 2];
  }
  float *cj = new float[m + 1];
  float *cB = new float[n + 1];  //基变量系数
  int *XB = new int[n + 1];  //用来标注基变量x的下标
  float *b = new float[n + 1];
  float *sigema = new float[n + 1];
  float *sita = new float[n + 1];
  //初始化
  for (int i = 0; i <= m; i++) {
    cj[i] = 0;
  }
  for (int i = 0; i <= n; i++) {
    cB[i] = 0;
    XB[i] = 0;
    b[i] = 0;
    sigema[i] = 0;
    sita[i] = 0;
  }
  cout << "请输入目标函数系数(用空格间开)：" << endl;
  for (int i = 1; i <= m; i++) {
    cin >> cj[i];
  }
  cout << "请输入各不等式的系数和常量(用空格间开)：" << endl;
  for (int i = 1; i <= n; i++) {
    cout << "不等式" << i << ": ";
    for (int j = 1; j <= m + 1; j++) {
      cin >> matrix[i][j];
    }
  }
  cout << "请输入目标函数中基变量下标：" << endl;
  for (int i = 1; i <= n; i++) {
    cin >> XB[i];
    cB[i] = cj[XB[i]];
    //常量
    b[i] = matrix[i][m + 1];
  }

  //计算检验数
  for (int i = 1; i <= m; i++) {
    sigema[i] = cj[i];
    for (int j = 1; j <= n; j++) {
      sigema[i] -= cB[j] * matrix[j][i];
    }
  }

  while (check(sigema, m) == 0) {
    //寻找入基变量
  float maxn = sigema[1];
  int sigema_xindex = 0;
  float sigema_xcoefficient = 0;
  for (int i = 1; i <= m; i++) {
    if (maxn <= sigema[i]) {
      maxn = sigema[i];
      sigema_xindex = i;
      sigema_xcoefficient = cj[i];
    }
  }
  //计算sita
  for (int i = 1; i <= n; i++) {
    if (matrix[i][sigema_xindex] > 0) {
      sita[i] = b[i] / matrix[i][sigema_xindex];
    }
    else {
      sita[i] = 9999; //表示sita值为负数
    }
  }
  //寻找出基变量
  float minn = sita[1];
  int sita_xindex = 0;
  for (int i = 1; i <= n; i++) {
    if (minn >= sita[i] && sita[i] > 0) {
      minn = sita[i];
      sita_xindex = i;
    }
  }
  //入基出基变换,先入基再出基
  //入基操作
  for (int i = 1; i <= n; i++) {
    if (i == sita_xindex) {
      XB[i] = sigema_xindex;
      cB[i] = sigema_xcoefficient;
      break;
    }
  }
  //出基计算
  //化1
  //cout << endl << "此处为化1的结果------" << endl;
  float mul1 = matrix[sita_xindex][sigema_xindex];
  for (int i = 1; i <= m; i++) {
    matrix[sita_xindex][i] /= mul1;
  }
  b[sita_xindex] /= mul1;
  //化0
  //cout << endl << "此处为化0的结果------" << endl;
  for (int i = 1; i <= n; i++) {
    if (i == sita_xindex) {
      continue;
    }
    float mul2 = matrix[i][sigema_xindex] / matrix[sita_xindex][sigema_xindex];
    for (int j = 1; j <= m; j++) {
      matrix[i][j] -= (matrix[sita_xindex][j] * mul2);
    }
    b[i] -= (b[sita_xindex] * mul2);
  }
  for (int i = 1; i <= n; i++) {
    if (i == sita_xindex) {
      continue;
    }
  }
  for (int i = 1; i <= m; i++) {
    sigema[i] = cj[i];
    for (int j = 1; j <= n; j++) {
      sigema[i] -= cB[j] * matrix[j][i];
    }
  }
  }
  float MaxZ = 0;
  float *result = new float[m + 1];
  for (int i = 0; i <= m; i++) {
    result[i] = 0;
  }
  for (int i = 1; i <= n; i++) {
    result[XB[i]] = b[i];
  }
  cout << "最优解为：X = (";
  for (int i = 1; i < m; i++) {
    cout << result[i] << ",";
  }
  cout << result[m] << ")" << endl;
  for (int i = 1; i <= m; i++) {
    MaxZ += result[i] * cj[i];
  }
  cout << "最优值为：MzxZ = " << MaxZ;
  return 0;
}

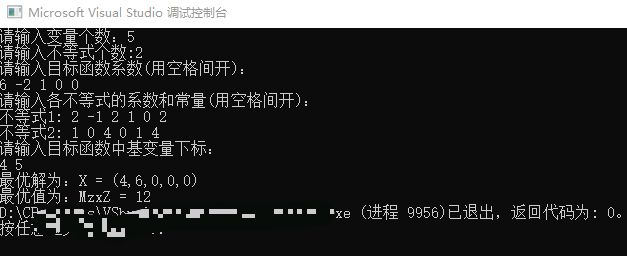
程序运行结果：

总结

到此这篇关于c++实现单纯形法现行规划问题的求解的文章就介绍到这了,更多相关c++单纯形法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！