基于Matlab实现鲸鱼优化算法的示例代码

目录

• 1.鲸鱼优化算法建模
• 1.1 包围猎物
• 1.2 螺旋狩猎
• 1.3 搜索猎物
• 1.4 算法流程图
• 2.Matlab代码实现
• 2.1 结果
• 2.2 代码

1.鲸鱼优化算法建模

鲸鱼优化算法(WOA)是澳大利亚学者Mirjaili等于2016年提出的群体智能优化算法，根据座头鲸的捕猎行为实现优化搜索的目的。其中，每个鲸鱼可以看作一个粒子，每个粒子作为不同的决策变量。WOA的实现过程主要包括包围猎物、螺旋狩猎和随机搜索3个阶段，其数学模型如下：

1.1 包围猎物

1.2 螺旋狩猎

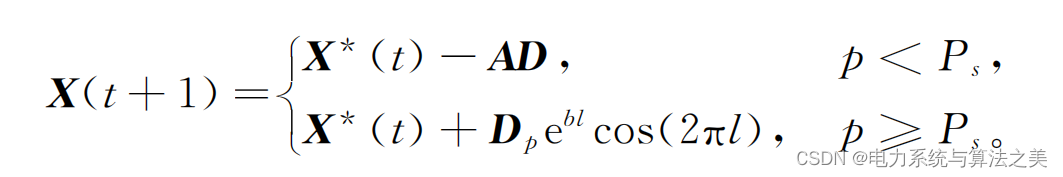
1.3 搜索猎物

1.4 算法流程图

2.Matlab代码实现

2.1 结果

2.2 代码

clear all
clc
 SearchAgents_no=30;
Function_name='F1'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)
% Max_iteration=500; % Maximum numbef of iterations
Max_iteration=500;
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);

[Best_score,Best_pos,WOABAT_cg_curve]=WOABAT(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);

 figure('Position',[269   240   660   290])
 %Draw search space
 subplot(1,2,1);
 func_plot(Function_name);
 title('Parameter space')
 xlabel('x_1');
 ylabel('x_2');
 zlabel([Function_name,'( x_1 , x_2 )'])

 %Draw objective space
 subplot(1,2,2);
 semilogy(WOABAT_cg_curve,'Color','r')
 title('Objective space')
 xlabel('Iteration');
 ylabel('Best score obtained so far');

 axis tight
 grid on
 box on
 legend('WOABAT')
%display(['The best solution obtained by WOABAT is : ', num2str(Best_pos)]);
 display(['The best optimal value of the objective funciton found by WOA is : ', num2str(Best_score)]);

 %display( num2str(Best_score));

% The Whale Optimization Algorithm
function [Leader_score,Leader_pos,Convergence_curve]=WOABAT(SearchAgents_no,Max_iter,lb,ub,dim,fobj)

% initialize position vector and score for the leader
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems

%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iter);

%bat algorithm addition
Qmin=0;         % Frequency minimum
Qmax=2;         % Frequency maximum
Q=zeros(SearchAgents_no,1);   % Frequency
v=zeros(SearchAgents_no,dim);   % Velocities
r=0.5;
A1=0.5;
t=0;% Loop counter
% summ=0;
% Main loop
while t<Max_iter
    for i=1:size(Positions,1)

        % Return back the search agents that go beyond the boundaries of the search space
        Flag4ub=Positions(i,:)>ub;
        Flag4lb=Positions(i,:)<lb;
        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;

        % Calculate objective function for each search agent
        fitness=fobj(Positions(i,:));

        % Update the leader
        if fitness<Leader_score % Change this to > for maximization problem
            Leader_score=fitness; % Update alpha
            Leader_pos=Positions(i,:);
        end

    end

    a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)

    % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)
    a2=-1+t*((-1)/Max_iter);

    % Update the Position of search agents
    for i=1:size(Positions,1)
        r1=rand(); % r1 is a random number in [0,1]
        r2=rand(); % r2 is a random number in [0,1]

        A=2*a*r1-a;
        C=2*r2;     

        b=1;
        l=(a2-1)*rand+1;   

       p = rand();        

        for j=1:size(Positions,2)

            if p<0.5   

                if abs(A)>=1

                             rand_leader_index = floor(SearchAgents_no*rand()+1);
                             X_rand = Positions(rand_leader_index, :);
                             Q(i)=Qmin+(Qmin-Qmax)*rand;
                             v(i,:)=v(i,j)+(X_rand(j)-Leader_pos(j))*Q(i);
                            z(i,:)= Positions(i,:)+ v(i,:);

                            %%%% problem
                                if rand>r
                                % The factor 0.001 limits the step sizes of random walks
                                z (i,:)=Leader_pos(j)+0.001*randn(1,dim);
                                end
                                     % Evaluate new solutions
                                    Fnew=fobj(z(i,:));
                                     % Update if the solution improves, or not too loud
                                    if (Fnew<=fitness) && (rand<A1)
                                       Positions(i,:)=z(i,:);
                                        fitness=Fnew;
                                    end

                elseif abs(A)<1
                             Q(i)=Qmin+(Qmin-Qmax)*rand;
                             v(i,:)=v(i,j)+(Positions(i,:)-Leader_pos(j))*Q(i);
                            z(i,:)= Positions(i,:)+ v(i,:);

                            %%%% problem
                                if rand>r
                                % The factor 0.001 limits the step sizes of random walks
                                z (i,:)=Leader_pos(j)+0.001*randn(1,dim);
                                end
                                     % Evaluate new solutions
                                    Fnew=fobj(z(i,:));
                                     % Update if the solution improves, or not too loud
                                    if (Fnew<=fitness) && (rand<A1)
                                       Positions(i,:)=z(i,:);
                                        fitness=Fnew;
                                    end
                end

            elseif p>=0.5

                distance2Leader=abs(Leader_pos(j)-Positions(i,j));
                % Eq. (2.5)
                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);
            end

        end
    end
    t=t+1;
    Convergence_curve(t)=Leader_score;
   [t Leader_score]

end

% This function draw the benchmark functions
function func_plot(func_name)

[lb,ub,dim,fobj]=Get_Functions_details(func_name);

switch func_name
    case 'F1'
        x=-100:2:100; y=x; %[-100,100]

    case 'F2'
        x=-100:2:100; y=x; %[-10,10]

    case 'F3'
        x=-100:2:100; y=x; %[-100,100]

    case 'F4'
        x=-100:2:100; y=x; %[-100,100]
    case 'F5'
        x=-200:2:200; y=x; %[-5,5]
    case 'F6'
        x=-100:2:100; y=x; %[-100,100]
    case 'F7'
        x=-1:0.03:1;  y=x  %[-1,1]
    case 'F8'
        x=-500:10:500;y=x; %[-500,500]
    case 'F9'
        x=-5:0.1:5;   y=x; %[-5,5]
    case 'F10'
        x=-20:0.5:20; y=x;%[-500,500]
    case 'F11'
        x=-500:10:500; y=x;%[-0.5,0.5]
    case 'F12'
        x=-10:0.1:10; y=x;%[-pi,pi]
    case 'F13'
        x=-5:0.08:5; y=x;%[-3,1]
    case 'F14'
        x=-100:2:100; y=x;%[-100,100]
    case 'F15'
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F16'
        x=-1:0.01:1; y=x;%[-5,5]
    case 'F17'
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F18'
        x=-5:0.06:5; y=x;%[-5,5]
    case 'F19'
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F20'
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F21'
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F22'
        x=-5:0.1:5; y=x;%[-5,5]
    case 'F23'
        x=-5:0.1:5; y=x;%[-5,5]
end    

L=length(x);
f=[];

for i=1:L
    for j=1:L
        if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
            f(i,j)=fobj([x(i),y(j)]);
        end
        if strcmp(func_name,'F15')==1
            f(i,j)=fobj([x(i),y(j),0,0]);
        end
        if strcmp(func_name,'F19')==1
            f(i,j)=fobj([x(i),y(j),0]);
        end
        if strcmp(func_name,'F20')==1
            f(i,j)=fobj([x(i),y(j),0,0,0,0]);
        end
        if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
            f(i,j)=fobj([x(i),y(j),0,0]);
        end
    end
end

surfc(x,y,f,'LineStyle','none');

end

function [lb,ub,dim,fobj] = Get_Functions_details(F)

switch F
    case 'F1'
        fobj = @F1;
        lb=-100;
        ub=100;
%         dim=30;
        dim=30;
    case 'F2'
        fobj = @F2;
        lb=-10;
        ub=10;
        dim=30;

    case 'F3'
        fobj = @F3;
        lb=-100;
        ub=100;
        dim=30;

    case 'F4'
        fobj = @F4;
        lb=-100;
        ub=100;
        dim=30;

    case 'F5'
        fobj = @F5;
        lb=-30;
        ub=30;
        dim=30;

    case 'F6'
        fobj = @F6;
        lb=-100;
        ub=100;
        dim=30;

    case 'F7'
        fobj = @F7;
        lb=-1.28;
        ub=1.28;
        dim=30;

    case 'F8'
        fobj = @F8;
        lb=-500;
        ub=500;
        dim=30;

    case 'F9'
        fobj = @F9;
        lb=-5.12;
        ub=5.12;
        dim=30;

    case 'F10'
        fobj = @F10;
        lb=-32;
        ub=32;
        dim=30;

    case 'F11'
        fobj = @F11;
        lb=-600;
        ub=600;
        dim=30;

    case 'F12'
        fobj = @F12;
        lb=-50;
        ub=50;
        dim=30;

    case 'F13'
        fobj = @F13;
        lb=-50;
        ub=50;
        dim=30;

    case 'F14'
        fobj = @F14;
        lb=-65.536;
        ub=65.536;
        dim=2;

    case 'F15'
        fobj = @F15;
        lb=-5;
        ub=5;
        dim=4;

    case 'F16'
        fobj = @F16;
        lb=-5;
        ub=5;
        dim=2;

    case 'F17'
        fobj = @F17;
        lb=[-5,0];
        ub=[10,15];
        dim=2;

    case 'F18'
        fobj = @F18;
        lb=-2;
        ub=2;
        dim=2;

    case 'F19'
        fobj = @F19;
        lb=0;
        ub=1;
        dim=3;

    case 'F20'
        fobj = @F20;
        lb=0;
        ub=1;
        dim=6;     

    case 'F21'
        fobj = @F21;
        lb=0;
        ub=10;
        dim=4;    

    case 'F22'
        fobj = @F22;
        lb=0;
        ub=10;
        dim=4;    

    case 'F23'
        fobj = @F23;
        lb=0;
        ub=10;
        dim=4;
end

end

% F1

function o = F1(x)
o=sum(x.^2);
end

% F2

function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end

% F3

function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
    o=o+sum(x(1:i))^2;
end
end

% F4

function o = F4(x)
o=max(abs(x));
end

% F5

function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end

% F6

function o = F6(x)
o=sum(abs((x+.5)).^2);
end

% F7

function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end

% F8

function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end

% F9

function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end

% F10

function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end

% F11

function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end

% F12

function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end

% F13

function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end

% F14

function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];

for j=1:25
    bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
    (30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
    o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
    o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F22

function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

o=0;
for i=1:7
    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end

% This function initialize the first population of search agents
function Positions=initialization(SearchAgents_no,dim,ub,lb)

Boundary_no= size(ub,2); % numnber of boundaries

% If the boundaries of all variables are equal and user enter a single
% number for both ub and lb
if Boundary_no==1
    Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end

% If each variable has a different lb and ub
if Boundary_no>1
    for i=1:dim
        ub_i=ub(i);
        lb_i=lb(i);
        Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
    end
end

以上就是基于Matlab实现鲸鱼优化算法的示例代码的详细内容，更多关于Matlab鲸鱼优化算法的资料请关注我们其它相关文章！