Java二叉树中LCA问题解决方法两则

目录

• 寻找公共祖先
• 方法一-普通解法
• 方法二-子问题

寻找公共祖先

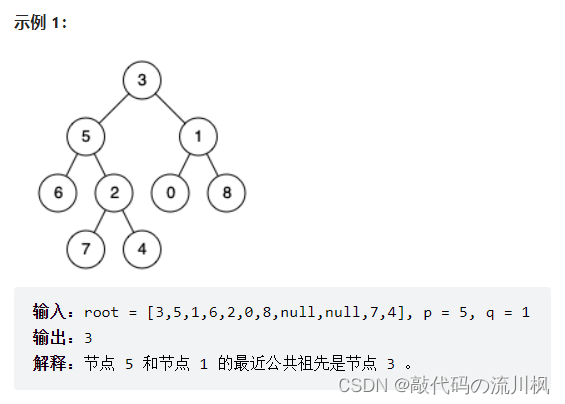
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

方法一-普通解法

思路：可以看作链表求交点的问题

首先需要找到到达两个节点的路径并用栈保存下来，然后让他们在同一起点，即路径长的先释放掉两个路径长的差值，然后两个栈依次弹出栈顶元素，若相同，则是这两个节点的公共祖先 。比较难的是怎样找到到达节点的路径，定义一个栈，从根节点开始遍历，栈先存储根节点，然后判断是否等于要找的节点，不等于则继遍历根节点的左右子树，左右子树又是新的根节点，如果左右子树不为要找的节点，则遍历他们的子树，还是找不到，则出栈，即这个节点不在要找的节点的路径里

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || p == null || q== null){
            return null;
        }
        Stack<TreeNode> stack1 = new Stack<>();
        getPath(root,p,stack1);
        Stack<TreeNode> stack2 = new Stack<>();
        getPath(root,q,stack2);
        int size1 = stack1.size();
        int size2 = stack2.size();
        int size = 0;
        if(size1 > size2){
             size = size1 - size2;
             while(size>0){
                 stack1.pop();
                 size--;
             }
        }
        else{
            size = size2 - size1;
            while(size>0){
                stack2.pop();
                size--;
            }
        }
        //起点已经相同
        while(stack1.peek() != stack2.peek()){
            stack2.pop();
            stack1.pop();
        }
        return stack1.peek();
    }
    public boolean getPath(TreeNode root,TreeNode node,Stack<TreeNode> stack){
        if(root == null || node == null){
            return false;
        }
        stack.push(root);
        if(root == node){
            return true;
        }
        boolean flag1 = getPath(root.left,node,stack);
        if(flag1 == true){
            return true;
        }
        boolean flag2 = getPath(root.right,node,stack);
        if(flag2 == true){
            return true;
        }
        stack.pop();
        return false;
    }
}

方法二-子问题

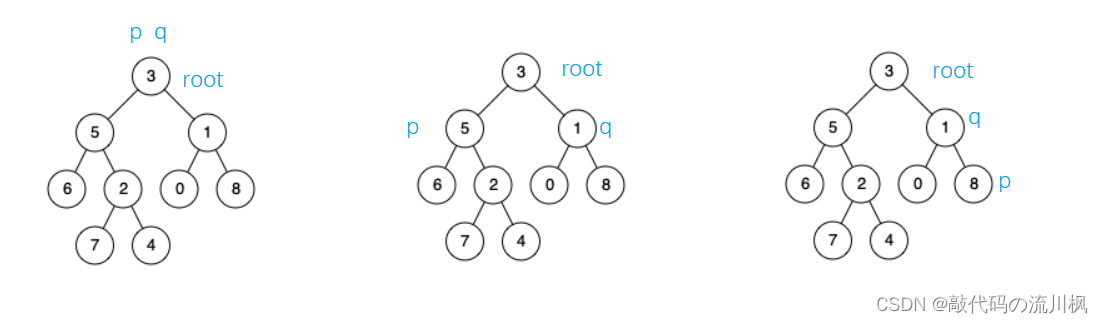
pq的分布为以上三种情况，pq为root时，就是公共祖先，若不是这种情况，则递归调用寻找root的左右子树节点是否有p或q。pq分布在root左右两侧时，root就是公共祖先，pq分布在单侧时，先找到的即为两个节点的公共祖先。子问题体现在寻找pq时，每个子树都会调用函数

代码

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       if(root == null ){
           return null;
       }
       if(root == p || root == q){
           return root;
       }
       TreeNode leftT = lowestCommonAncestor(root.left,p,q);
       TreeNode rightT = lowestCommonAncestor(root.right,p,q);
       if(leftT != null && rightT != null){
           return root;
       }
       else if(leftT != null){
           return leftT;
       }
       else if(rightT != null){
           return rightT;
       }
       else{
           return null;
       }
    }
}

到此这篇关于Java二叉树中LCA问题解决方法两则的文章就介绍到这了,更多相关Java二叉树中LCA问题内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！