一篇文章教你用Python绘画一个太阳系
目录
- 日地月三体
- 日地火
- 太阳系
你们要的3D太阳系
图片上传之后不知为何帧率降低了许多。。。
日地月三体
所谓三体,就是三个物体在重力作用下的运动。由于三点共面,所以三个质点仅在重力作用下的运动轨迹也必然无法逃离平面。
三体运动所遵循的规律就是古老而经典的万有引力
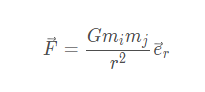
则对于 m i 而言,
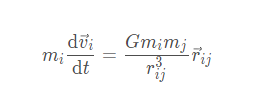
且

将其写为差分形式
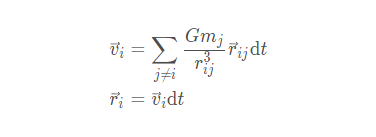
由于我们希望观察三体运动的复杂形式,而不关系其随对应的宇宙星体,所以不必考虑单位制,将其在二维平面坐标系中拆分,则

#后续代码主要更改这里的参数 m = [1.33e20,3.98e14,4.9e12] x = np.array([0,1.5e11,1.5e11+3.8e8]) y = np.array([0,0,0]) u = np.array([0,0,0]) v = np.array([0,2.88e4,1.02e3])
由于地月之间的距离相对于日地距离太近,所以在画图的时候将其扩大100倍,得到图像
尽管存在误差,但最起码看到了地球围绕太阳转,月球围绕地球转。。。代码为
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
m = [1.33e20,3.98e14,4.9e12]
x = np.array([0,1.5e11,1.5e11+3.8e8])
y = np.array([0.0,0,0])
u = np.array([0.0,0,0])
v = np.array([0,2.88e4,2.88e4+1.02e3])
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(xlim=(-2e11,2e11),ylim=(-2e11,2e11))
ax.grid()
trace0, = ax.plot([],[],'-', lw=0.5)
trace1, = ax.plot([],[],'-', lw=0.5)
trace2, = ax.plot([],[],'-', lw=0.5)
pt0, = ax.plot([x[0]],[y[0]] ,marker='o')
pt1, = ax.plot([x[0]],[y[0]] ,marker='o')
pt2, = ax.plot([x[0]],[y[0]] ,marker='o')
k_text = ax.text(0.05,0.85,'',transform=ax.transAxes)
textTemplate = 't = %.3f days\n'
N = 1000
dt = 36000
ts = np.arange(0,N*dt,dt)/3600/24
xs,ys = [],[]
for _ in ts:
x_ij = (x-x.reshape(3,1))
y_ij = (y-y.reshape(3,1))
r_ij = np.sqrt(x_ij**2+y_ij**2)
for i in range(3):
for j in range(3):
if i!=j :
u[i] += (m[j]*x_ij[i,j]*dt/r_ij[i,j]**3)
v[i] += (m[j]*y_ij[i,j]*dt/r_ij[i,j]**3)
x += u*dt
y += v*dt
xs.append(x.tolist())
ys.append(y.tolist())
xs = np.array(xs)
ys = np.array(ys)
def animate(n):
trace0.set_data(xs[:n,0],ys[:n,0])
trace1.set_data(xs[:n,1],ys[:n,1])
#绘图时的地月距离扩大100倍,否则看不清
tempX2S = xs[:n,1]+100*(xs[:n,2]-xs[:n,1])
tempY2S = ys[:n,1]+100*(ys[:n,2]-ys[:n,1])
trace2.set_data(tempX2S,tempY2S)
pt0.set_data([xs[n,0]],[ys[n,0]])
pt1.set_data([xs[n,1]],[ys[n,1]])
tempX = xs[n,1]+100*(xs[n,2]-xs[n,1])
tempY = ys[n,1]+100*(ys[n,2]-ys[n,1])
pt2.set_data([tempX],[tempY])
k_text.set_text(textTemplate % ts[n])
return trace0, trace1, trace2, pt0, pt1, pt2, k_text
ani = animation.FuncAnimation(fig, animate,
range(N), interval=10, blit=True)
plt.show()
ani.save("3.gif")
日地火

m = [1.33e20,3.98e14,4.28e13]
x = np.array([0,1.5e11,2.28e11])
y = np.array([0.0,0,0])
u = np.array([0.0,0,0])
v = np.array([0,2.88e4,2.4e4])
### 由于火星离地球很远,所以不必再改变尺度
def animate(n):
trace0.set_data(xs[:n,0],ys[:n,0])
trace1.set_data(xs[:n,1],ys[:n,1])
trace2.set_data(xs[:n,2],ys[:n,2])
pt0.set_data([xs[n,0]],[ys[n,0]])
pt1.set_data([xs[n,1]],[ys[n,1]])
pt2.set_data([xs[n,2]],[ys[n,2]])
k_text.set_text(textTemplate % ts[n])
return trace0, trace1, trace2, pt0, pt1, pt2, k_text
得到
这个运动要比月球的运动简单得多——前提是开上帝视角,俯瞰太阳系。如果站在地球上观测火星的运动,那么这个运动可能相当带感
所以这都能找到规律,托勒密那帮人也真够有才的。
太阳系
由于太阳和其他星体之间的质量相差悬殊,所以太阳系内的多体运动,都将退化为二体问题,甚至如果把太阳当作不动点,那就成了单体问题了。
尽管如此,我们还是尽可能地模仿一下太阳系的运动情况
| 质量 | 半长轴(AU) | 平均速度(km/s) | |
|---|---|---|---|
| 水星 | 0.055 | 0.387 | 47.89 |
| 金星 | 0.815 | 0.723 | 35.03 |
| 地球 | 1 | 1 | 29.79 |
| 火星 | 0.107 | 1.524 | 24.13 |
| 木星 | 317.8 | 5.203 | 13.06 |
| 土星 | 95.16 | 9.537 | 9.64 |
| 天王星 | 14.54 | 19.19 | 6.81 |
| 海王星 | 17.14 | 30.07 | 5.43 |
| 冥王星 |
除了水星偏心率为0.2,对黄道面倾斜为7°之外,其余行星的偏心率皆小于0.1,且对黄道面倾斜普遍小于4°。由于水星的轨道太小,偏不偏心其实都不太看得出来,所以就当它是正圆也无所谓了,最后得图
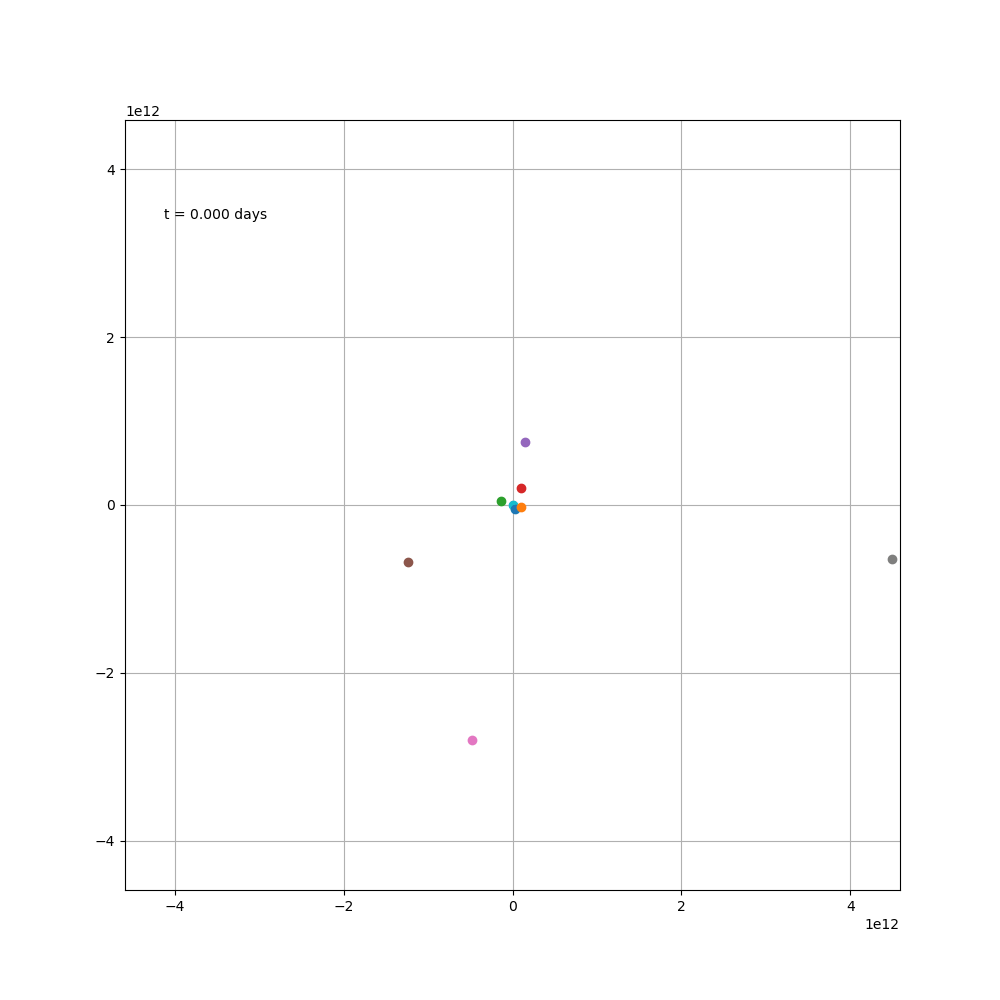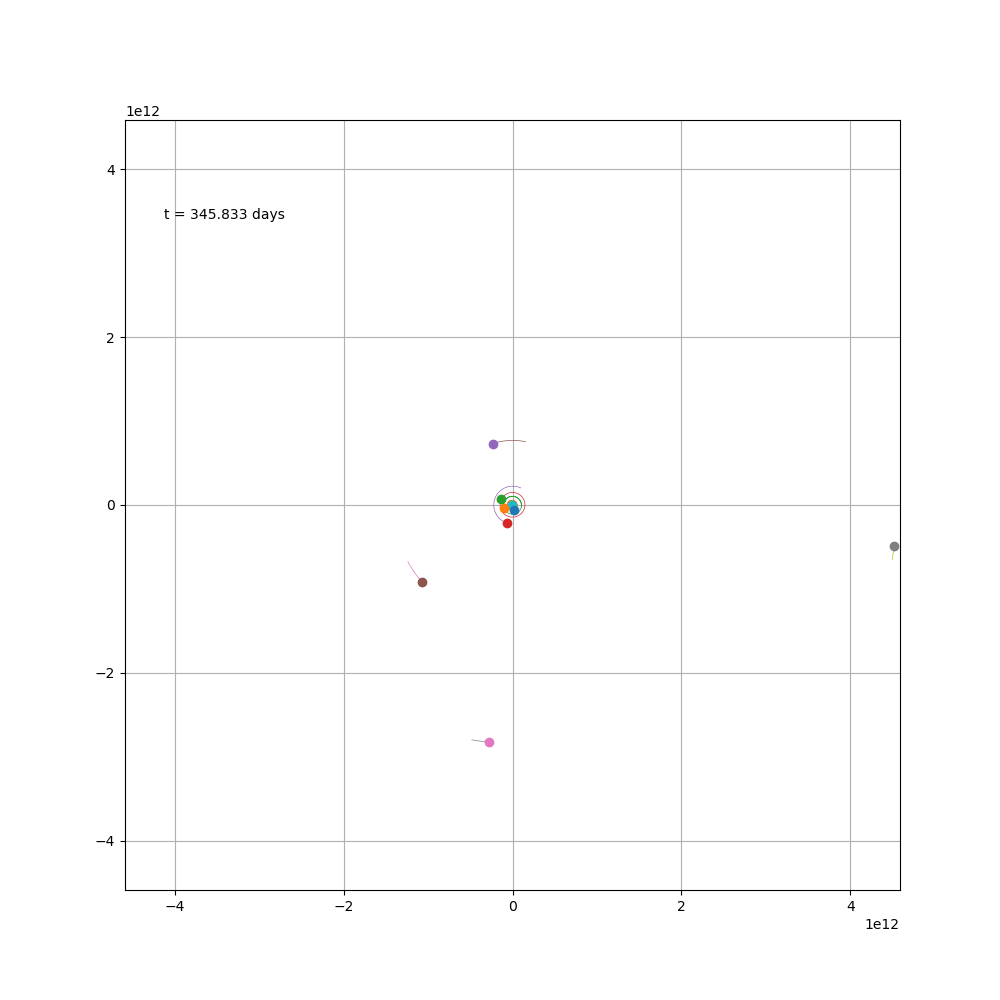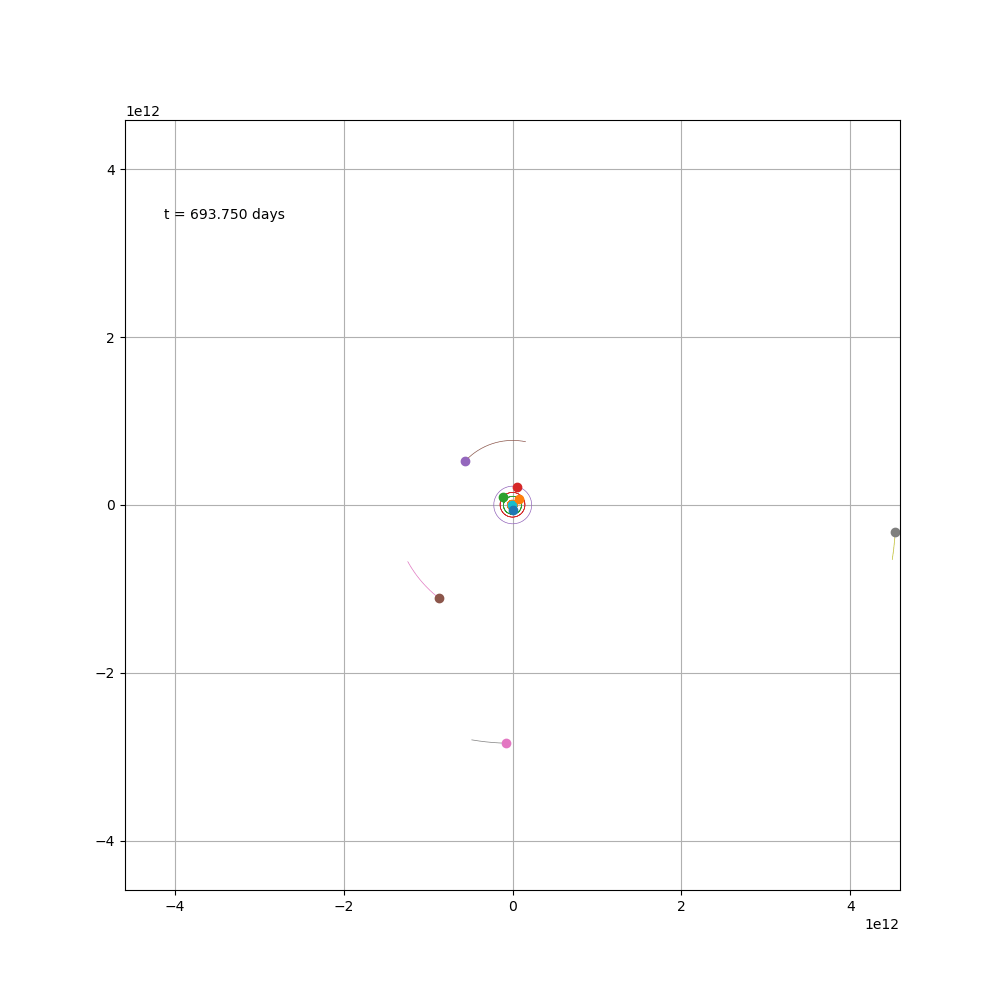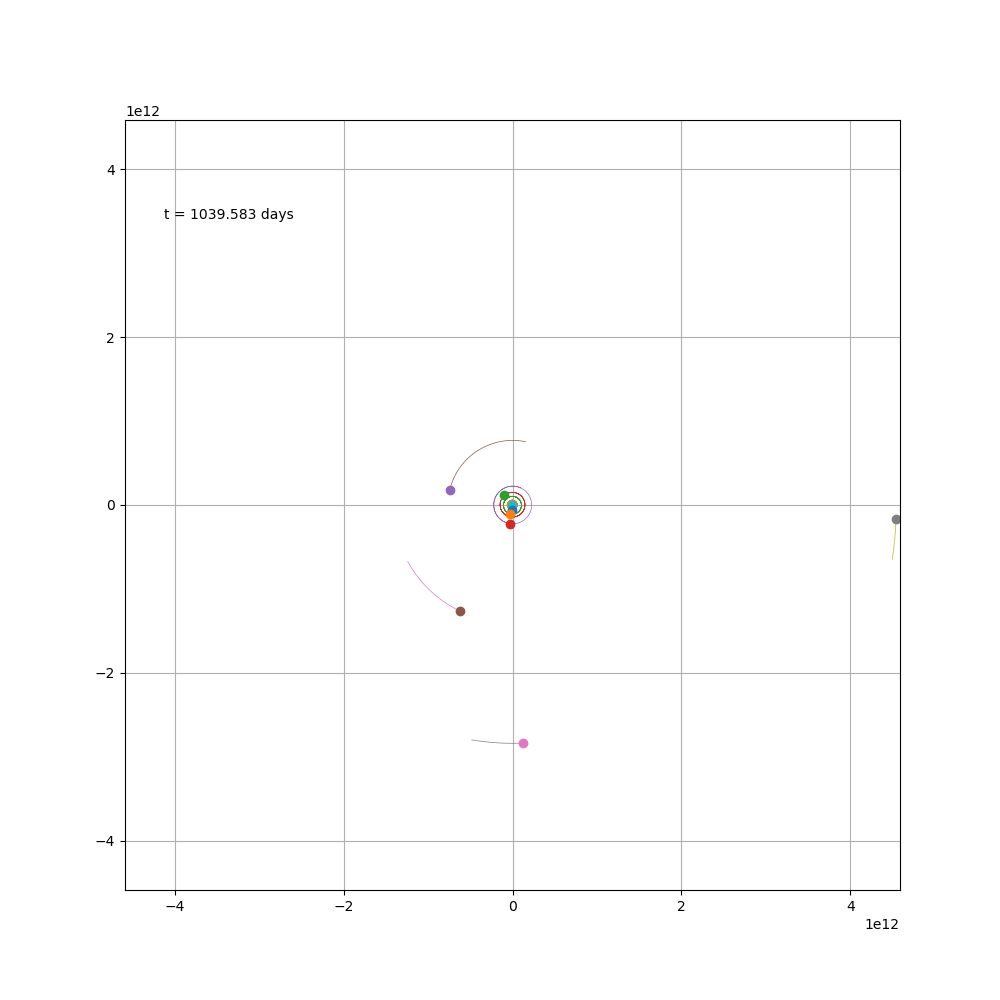
au,G,RE,ME = 1.48e11,6.67e-11,1.48e11,5.965e24
m = np.array([3.32e5,0.055,0.815,1,
0.107,317.8,95.16,14.54,17.14])*ME*6.67e-11
r = np.array([0,0.387,0.723,1,1.524,5.203,
9.537,19.19,30.7])*RE
theta = np.random.rand(9)*np.pi*2
x = r*np.cos(theta)
y = r*np.sin(theta)
v = np.array([0,47.89,35.03,29.79,
24.13,13.06,9.64,6.81,5.43])*1000
u = -v*np.sin(theta)
v = v*np.cos(theta)
name = "solar.gif"
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(xlim=(-31*RE,31*RE),ylim=(-31*RE,31*RE))
ax.grid()
traces = [ax.plot([],[],'-', lw=0.5)[0] for _ in range(9)]
pts = [ax.plot([],[],marker='o')[0] for _ in range(9)]
k_text = ax.text(0.05,0.85,'',transform=ax.transAxes)
textTemplate = 't = %.3f days\n'
N = 500
dt = 3600*50
ts = np.arange(0,N*dt,dt)
xs,ys = [],[]
for _ in ts:
x_ij = (x-x.reshape(len(m),1))
y_ij = (y-y.reshape(len(m),1))
r_ij = np.sqrt(x_ij**2+y_ij**2)
for i in range(len(m)):
for j in range(len(m)):
if i!=j :
u[i] += (m[j]*x_ij[i,j]*dt/r_ij[i,j]**3)
v[i] += (m[j]*y_ij[i,j]*dt/r_ij[i,j]**3)
x += u*dt
y += v*dt
xs.append(x.tolist())
ys.append(y.tolist())
xs = np.array(xs)
ys = np.array(ys)
def animate(n):
for i in range(9):
traces[i].set_data(xs[:n,i],ys[:n,i])
pts[i].set_data(xs[n,i],ys[n,i])
k_text.set_text(textTemplate % (ts[n]/3600/24))
return traces+pts+[k_text]
ani = animation.FuncAnimation(fig, animate,
range(N), interval=10, blit=True)
plt.show()
ani.save(name)
由于外圈的行星轨道又长速度又慢,而内层的刚好相反,所以这个图很难兼顾,观感上也不太好看。
如果只画出木星之前的星体,顺便加上小行星带,可能会好一些。

通过这个图就能看出来,有一颗小行星被木星弹了过来,直冲冲地向地球赶来,幸好又被太阳弹了出去,可见小行星还是挺危险的,好在这只是个假想图。
赞 (0)

