Python实现求解斐波那契第n项的解法(包括矩阵乘法＋快速幂)

斐波那契数列

首先我们来定义一下斐波那契数列：

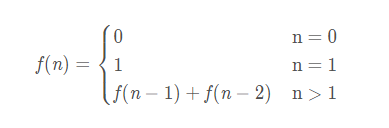
即数列的第0项：

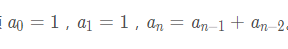
算法一：递归

递归计算的节点个数是O(2ⁿ)的级别的，效率很低，存在大量的重复计算。

比如：

f(10) = f(9) + f(8)

f(9) = f(8) + f(7) 重复 8

f(8) = f(7) + f(6) 重复 7

时间复杂度是O(2ⁿ),极慢

def F1(n):
    if n <= 1: return max(n, 0)  # 前两项
    return F1(n-1)+F1(n-2)  # 递归

算法二：记忆化搜索

开一个大数组记录中间结果，如果一个状态被计算过，则直接查表，否则再递归计算。

总共有 n 个状态，计算每个状态的复杂度是 O(1)，所以时间复杂度是 O(n)。但由于是递归计算，递归层数太多会爆栈。

res = [None]*100000
def F2(n):
    if n <= 1: return max(n, 0)
    if res[n]: return res[n]  # 如果已存在则直接查找返回结果
    res[n] = F2(n-1)+F2(n-2)  # 不存在则计算
    return res[n]

算法三：递推

开一个大数组，记录每个数的值。用循环递推计算。

总共计算 n 个状态，所以时间复杂度是 O(n)。但需要开一个长度是 n 的数组，内存将成为瓶颈。

def F3(n):
    if n <= 1: return max(n, 0)
    res = [0, 1]
    for i in range(2,n+1):
        res.append(res[i-1]+res[i-2])
    return res[n]

算法四：递归+滚动变量

比较优秀的一种解法。仔细观察我们会发现，递推时我们只需要记录前两项的值即可，没有必要记录所有值，所以我们可以用滚动变量递推。

时间复杂度还是 O(n)，但空间复杂度变成了O(1)。

def F4(n):
    if n <= 1: return max(n, 0)
    fn, f0, f1 = 0, 1, 0  # fn为最终结果，f0为第0项，f1为第一项，
    for i in range(2, n+1):
        fn = f0 + f1  # 前两项和
        f0, f1 = f1, fn  # 递推变量
    return fn

算法五：矩阵乘法+快速幂

利用矩阵运算的性质将通项公式变成幂次形式，然后用平方倍增（快速幂）的方法求解第 n 项。

先说通式：

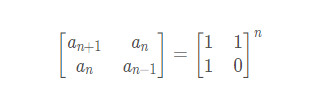
利用数学归纳法证明：

这里的a0,a1,a2是对应斐波那契的第几项

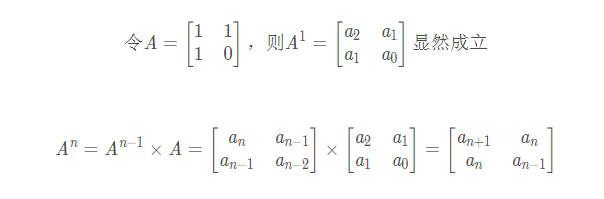
证毕。

所以我们想要的得到An，只需要求得Aⁿ，然后取第一行第二个元素即可。

如果只是简单的从0开始循环求n次方，时间复杂度仍然是O(n)，并不比前面的快。我们可以考虑乘方的如下性质，即快速幂：

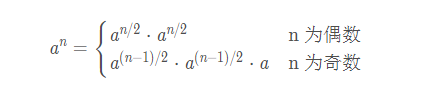
这样只需要 logn 次运算即可得到结果，时间复杂度为 O(logn)

def mul(a, b):  # 首先定义二阶矩阵乘法运算
    c = [[0, 0], [0, 0]]  # 定义一个空的二阶矩阵，存储结果
    for i in range(2):  # row
        for j in range(2):  # col
            for k in range(2):  # 新二阶矩阵的值计算
                c[i][j] += a[i][k] * b[k][j]
    return c
def F5(n):
    if n <= 1: return max(n, 0)
    res = [[1, 0], [0, 1]]  # 单位矩阵，等价于1
    A = [[1, 1], [1, 0]]  # A矩阵
    while n:
        if n & 1: res = mul(res, A)  # 如果n是奇数，或者直到n=1停止条件
        A = mul(A, A)  # 快速幂
        n >>= 1  # 整除2，向下取整
    return res[0][1]

总的来说不是很难，适合扩展思路。更多关于Python的资料请关注我们其它相关文章！希望大家以后多多支持我们！

赞 (0)

相关推荐

  • python 如何将两个实数矩阵合并为一个复数矩阵

    问题描述: 有时需要把两个实数矩阵,一个作为实部,一个作为虚部,合并为一个复数矩阵,该如何操作? 解决办法: 假如是在第二个维度上进行合并(real: Data[:, 0, :, :] imag: Data[:, 1, :, :]),有两种方法 第一种. result = Data[:, 0, :, :] + 1j*Data[:, 1, :, :] 第二种. result = 1j*Data[:, 1, :, :] result += Data[:, 0, :, :] 第二种方法更节省内存~ 补

  • Python:合并两个numpy矩阵的实现

    numpy是Python用来科学计算的一个非常重要的库,numpy主要用来处理一些矩阵对象,可以说numpy让Python有了Matlab的味道. 如何利用numpy来合并两个矩阵呢?我们可以利用numpy向我们提供的两个函数来进行操作. #hstack()在行上合并 np.hstack((a,b)) #vstack()在列上合并 np.vstack((a,b)) 以上a,b分别为两个numpy矩阵.hstack在行上合并,vstack在列上合并. 这篇Python:合并两个numpy矩阵的实现

  • Python numpy大矩阵运算内存不足如何解决

    程序运行,产生如下结果,然后进程终止,导致这一结果的原因很有可能是内存爆炸. 当两个较大的 (e.g., 10000*10000 维)ndarray 做运算(加法,or 乘法)时,很容易出现这样的结果. 解决办法: 大多数情况下,这种大矩阵都是稀疏的.尽可能地利用稀疏计算的方式,例如稀疏矩阵,或者只计算非 0 位置的值. 如果都是整数运算,可以设置 dtype=int,而非 dtype=float, 可以省下不少空间. linux 系统下,使用 top 命令,可以很容易地看到内存(%MEM) 的

  • python实现由数组生成对称矩阵

    在实际应用中,经常会遇上这样的小需求:根据一段给定的数组,生成由这一段数组值构成的对称矩阵. 例如,给定数组[1,2,3,4,5,6,7,8,9,10],要求生成如下的矩阵: [[0,1,2,3,4], [1,0,5,6,7], [2,5,0,8,9], [3,6,8,0,10], [4,7,9,10,0]] 其中,对角元全为0,该类型的矩阵完全由给定的数组决定. 笔者给出实现以上功能的一种python参考代码如下: def semi_to_full(m): import numpy as np

  • Python计算矩阵的和积的实例详解

    python的numpy库提供矩阵运算的功能,因此我们在需要矩阵运算的时候,需要导入numpy的包. 一.numpy的导入和使用 from numpy import *;#导入numpy的库函数 import numpy as np; #这个方式使用numpy的函数时,需要以np.开头. 二.矩阵的创建 由一维或二维数据创建矩阵 from numpy import *; a1=array([1,2,3]); a1=mat(a1); 创建常见的矩阵 data1=mat(zeros((3,3)));

  • Python 如何求矩阵的逆

    Python 如何求矩阵的逆

    我就废话不多说了,大家还是直接看代码吧~ import numpy as np kernel = np.array([1, 1, 1, 2]).reshape((2, 2)) print(kernel) print(np.linalg.inv(kernel)) 注意,Singular matrix奇异矩阵不可求逆 补充:python+numpy中矩阵的逆和伪逆的区别 定义: 对于矩阵A,如果存在一个矩阵B,使得AB=BA=E,其中E为与A,B同维数的单位阵,就称A为可逆矩阵(或者称A可逆),并称

  • python用分数表示矩阵的方法实例

    python用分数表示矩阵的方法实例

    前言 在机器学习中,我们会经常和矩阵打交道.在矩阵的运算中,python默认的输出是浮点数,但是如果我们想要矩阵的元素以分数的形式显示,可以通过添加一行代码来实现. 1.函数及参数解释 set_printoptions()--控制输出方式 formatter--通用格式化输出 Fraction(x).limit_denominator(y)--返回一个分母不大于y且最接近x的分数 2.代码实现 from fractions import Fraction import numpy as np #

  • Python实现求解斐波那契第n项的解法(包括矩阵乘法＋快速幂)

    Python实现求解斐波那契第n项的解法(包括矩阵乘法＋快速幂)

    斐波那契数列 首先我们来定义一下斐波那契数列: 即数列的第0项: 算法一:递归 递归计算的节点个数是O(2ⁿ)的级别的,效率很低,存在大量的重复计算. 比如: f(10) = f(9) + f(8) f(9) = f(8) + f(7) 重复 8 f(8) = f(7) + f(6) 重复 7 时间复杂度是O(2ⁿ),极慢 def F1(n): if n <= 1: return max(n, 0) # 前两项 return F1(n-1)+F1(n-2) # 递归 算法二:记忆化搜索 开一个大

  • Java打印斐波那契前N项的实现示例

    题外 由于idea原因 用注解test无法在控制台上输入所以写死到程序里了,版本都30.9102了为什么还是这样啊,intelJ你们该反思了!!! 用intelJ IDEA的小伙伴有遇到这种测试情况吗,如果项目上有测试用例需要自己单元测试,怎么解决控制台输入问题(@test情况下),直接改main方法的那个就算了.~~ 斐波那契的认识 斐波那契数列前2项为1,从第3项开始为该项的前2项和. eg:1,1,2,3,5,8- f(n)=f(n-1)+f(n-2) 代码参考 import org.ju

  • SpringBoot搭建Dubbo项目实现斐波那契第n项详解

    SpringBoot搭建Dubbo项目实现斐波那契第n项详解

    目录 step1 新建项目 step2 新建需要的包和接口以及实现类 step3 在两个项目的resource下新建配置文件 step4 代码编写 导入依赖 provider consumer 端口冲突更改 step5 运行 step1 新建项目 方法1:直接在IDEA里新建如图: 方法2:在start.spring.io新建 可能有的小朋友已经发现了,第一种方式的Server URL就是第二个的网站,都是一样的 要新建两个项目,第一个项目如上图所示,第二个项目只需要将provider改为con

  • C语言求Fibonacci斐波那契数列通项问题的解法总结

    C语言求Fibonacci斐波那契数列通项问题的解法总结

    一:递归实现   使用公式f[n]=f[n-1]+f[n-2],依次递归计算,递归结束条件是f[1]=1,f[2]=1. 二:数组实现   空间复杂度和时间复杂度都是0(n),效率一般,比递归来得快. 三:vector<int>实现   时间复杂度是0(n),时间复杂度是0(1),就是不知道vector的效率高不高,当然vector有自己的属性会占用资源. 四:queue<int>实现   当然队列比数组更适合实现斐波那契数列,时间复杂度和空间复杂度和vector<int&g

  • 打印菱形以及斐波纳契数列的几种解法介绍

    打印菱形以及斐波纳契数列的几种解法介绍

    1.编写程序,打印*菱形推出第i行要打印的空白个数及*号个数,用for循环依次打印各行 复制代码 代码如下: #include<stdio.h>//总共要打印2*n-1行,逐行打印void print1(int n){ int i,j; for(i=1;i<=n;i++){//打印1至n行  for(j=1;j<=n-i;j++)//打印n-i个空格      printf(" ");  for(j=1;j<=2*i-1;j++)//打印2*i-1个*号 

  • 详解python使用递归、尾递归、循环三种方式实现斐波那契数列

    在最开始的时候所有的斐波那契代码都是使用递归的方式来写的,递归有很多的缺点,执行效率低下,浪费资源,还有可能会造成栈溢出,而递归的程序的优点也是很明显的,就是结构层次很清晰,易于理解 可以使用循环的方式来取代递归,当然也可以使用尾递归的方式来实现. 尾递归就是从最后开始计算, 每递归一次就算出相应的结果, 也就是说, 函数调用出现在调用者函数的尾部, 因为是尾部, 所以根本没有必要去保存任何局部变量. 直接让被调用的函数返回时越过调用者, 返回到调用者的调用者去.尾递归就是把当前的运算结果(或路

  • 用C语言求解第N项斐波那契数列问题

    目录 求解第N项斐波那契数列 求解斐波那契数列的前n项并输出及兔子繁殖问题 斐波那契数列的定义 算法思路 代码实现 兔子繁殖问题 求解第N项斐波那契数列 斐波那契数列指的是这样一个数列:1,1,2,3,5,8,13,21,34,55,89... 这个数列从第3项开始,每一项都等于前两项之和.斐波那契数列,又称黄金分割数列,显然它又是一个线性递推数列,由数学家莱昂纳多·斐波纳契首次引入此概念.在现代的物理,化学,生物等诸多领域,皆有重大影响. 在此求解过程中,我用了if 语句和for循环.话不多说

  • 如何使用Python实现斐波那契数列

    如何使用Python实现斐波那契数列

    斐波那契数列(Fibonacci)最早由印度数学家Gopala提出,而第一个真正研究斐波那契数列的是意大利数学家 Leonardo Fibonacci,斐波那契数列的定义很简单,用数学函数可表示为: 数列从0和1开始,之后的数由前两个数相加而得出,例如斐波那契数列的前10个数是:0, 1, 1, 2, 3, 5, 8, 13, 21, 34. 用 Python 实现斐波那契数列常见的写法有三种,各算法的执行效率也有很大差别,在面试中也会偶尔会被问到,通常面试的时候不是让你简单的用递归写写就完了,

  • Python实现斐波那契数列的多种写法总结

    目录 1.for循环 2.while循环 3.使用递归 4.递归+for循环 5.递归+while循环 6.递归+定义函数+for循环 7.指定列表 趣方程求解 pandas 每日一练 斐波那契数列——经典例子,永不过时!!! 1.for循环 def fibonacci1(n): a, b = 0, 1 for i in range(n): a, b = b, a+b print(a) fibonacci1(3) 或 def fib1(w): a, b = 1, 1 for i in range

  • python实现斐波那契递归函数的方法

    本文以一个简单的实例讲述了python实现斐波那契数列数列递归函数的方法,代码精简易懂.分享给大家供大家参考之用. 主要函数代码如下: def fab(n): if n==1: return 1 if n==0: return 0 else: result=int(fab(n-1))+int(fab(n-2)) return result 测试代码如下: for i in range(10): print fab(i) 希望本文所述对大家Python程序设计的学习有所帮助.

随机推荐