python实现决策树C4.5算法详解(在ID3基础上改进)

一、概论

C4.5主要是在ID3的基础上改进，ID3选择（属性）树节点是选择信息增益值最大的属性作为节点。而C4.5引入了新概念“信息增益率”,C4.5是选择信息增益率最大的属性作为树节点。

二、信息增益

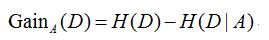
以上公式是求信息增益率（ID3的知识点）

三、信息增益率

信息增益率是在求出信息增益值在除以。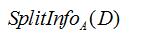

例如下面公式为求属性为“outlook”的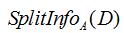值：

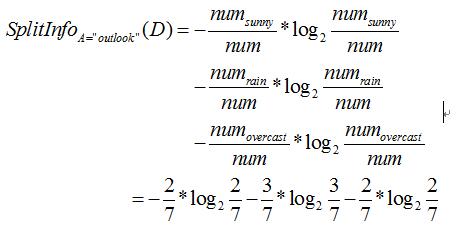
四、C4.5的完整代码

from numpy import *
from scipy import *
from math import log
import operator

#计算给定数据的香浓熵：
def calcShannonEnt(dataSet):
 numEntries = len(dataSet)
 labelCounts = {} #类别字典（类别的名称为键，该类别的个数为值）
 for featVec in dataSet:
  currentLabel = featVec[-1]
  if currentLabel not in labelCounts.keys(): #还没添加到字典里的类型
   labelCounts[currentLabel] = 0;
  labelCounts[currentLabel] += 1;
 shannonEnt = 0.0
 for key in labelCounts: #求出每种类型的熵
  prob = float(labelCounts[key])/numEntries #每种类型个数占所有的比值
  shannonEnt -= prob * log(prob, 2)
 return shannonEnt; #返回熵

#按照给定的特征划分数据集
def splitDataSet(dataSet, axis, value):
 retDataSet = []
 for featVec in dataSet: #按dataSet矩阵中的第axis列的值等于value的分数据集
  if featVec[axis] == value:  #值等于value的，每一行为新的列表（去除第axis个数据）
   reducedFeatVec = featVec[:axis]
   reducedFeatVec.extend(featVec[axis+1:])
   retDataSet.append(reducedFeatVec)
 return retDataSet #返回分类后的新矩阵

#选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
 numFeatures = len(dataSet[0])-1 #求属性的个数
 baseEntropy = calcShannonEnt(dataSet)
 bestInfoGain = 0.0; bestFeature = -1
 for i in range(numFeatures): #求所有属性的信息增益
  featList = [example[i] for example in dataSet]
  uniqueVals = set(featList) #第i列属性的取值（不同值）数集合
  newEntropy = 0.0
  splitInfo = 0.0;
  for value in uniqueVals: #求第i列属性每个不同值的熵*他们的概率
   subDataSet = splitDataSet(dataSet, i , value)
   prob = len(subDataSet)/float(len(dataSet)) #求出该值在i列属性中的概率
   newEntropy += prob * calcShannonEnt(subDataSet) #求i列属性各值对于的熵求和
   splitInfo -= prob * log(prob, 2);
  infoGain = (baseEntropy - newEntropy) / splitInfo; #求出第i列属性的信息增益率
  print infoGain;
  if(infoGain > bestInfoGain): #保存信息增益率最大的信息增益率值以及所在的下表（列值i）
   bestInfoGain = infoGain
   bestFeature = i
 return bestFeature 

#找出出现次数最多的分类名称
def majorityCnt(classList):
 classCount = {}
 for vote in classList:
  if vote not in classCount.keys(): classCount[vote] = 0
  classCount[vote] += 1
 sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgetter(1), reverse=True)
 return sortedClassCount[0][0] 

#创建树
def createTree(dataSet, labels):
 classList = [example[-1] for example in dataSet]; #创建需要创建树的训练数据的结果列表（例如最外层的列表是[N, N, Y, Y, Y, N, Y]）
 if classList.count(classList[0]) == len(classList): #如果所有的训练数据都是属于一个类别，则返回该类别
  return classList[0];
 if (len(dataSet[0]) == 1): #训练数据只给出类别数据（没给任何属性值数据），返回出现次数最多的分类名称
  return majorityCnt(classList);

 bestFeat = chooseBestFeatureToSplit(dataSet); #选择信息增益最大的属性进行分（返回值是属性类型列表的下标）
 bestFeatLabel = labels[bestFeat] #根据下表找属性名称当树的根节点
 myTree = {bestFeatLabel:{}} #以bestFeatLabel为根节点建一个空树
 del(labels[bestFeat]) #从属性列表中删掉已经被选出来当根节点的属性
 featValues = [example[bestFeat] for example in dataSet] #找出该属性所有训练数据的值（创建列表）
 uniqueVals = set(featValues) #求出该属性的所有值得集合（集合的元素不能重复）
 for value in uniqueVals: #根据该属性的值求树的各个分支
  subLabels = labels[:]
  myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) #根据各个分支递归创建树
 return myTree #生成的树

#实用决策树进行分类
def classify(inputTree, featLabels, testVec):
 firstStr = inputTree.keys()[0]
 secondDict = inputTree[firstStr]
 featIndex = featLabels.index(firstStr)
 for key in secondDict.keys():
  if testVec[featIndex] == key:
   if type(secondDict[key]).__name__ == 'dict':
    classLabel = classify(secondDict[key], featLabels, testVec)
   else: classLabel = secondDict[key]
 return classLabel 

#读取数据文档中的训练数据（生成二维列表）
def createTrainData():
 lines_set = open('../data/ID3/Dataset.txt').readlines()
 labelLine = lines_set[2];
 labels = labelLine.strip().split()
 lines_set = lines_set[4:11]
 dataSet = [];
 for line in lines_set:
  data = line.split();
  dataSet.append(data);
 return dataSet, labels

#读取数据文档中的测试数据（生成二维列表）
def createTestData():
 lines_set = open('../data/ID3/Dataset.txt').readlines()
 lines_set = lines_set[15:22]
 dataSet = [];
 for line in lines_set:
  data = line.strip().split();
  dataSet.append(data);
 return dataSet

myDat, labels = createTrainData()
myTree = createTree(myDat,labels)
print myTree
bootList = ['outlook','temperature', 'humidity', 'windy'];
testList = createTestData();
for testData in testList:
 dic = classify(myTree, bootList, testData)
 print dic

五、C4.5与ID3的代码区别

如上图，C4.5主要在第52、53行代码与ID3不同（ID3求的是信息增益，C4.5求的是信息增益率）。

六、训练、测试数据集样例

训练集:

 outlook temperature humidity windy
 ---------------------------------------------------------
 sunny  hot    high   false   N
 sunny  hot    high   true   N
 overcast hot    high   false   Y
 rain  mild   high   false   Y
 rain  cool   normal  false   Y
 rain  cool   normal  true   N
 overcast cool   normal  true   Y

测试集
 outlook temperature humidity windy
 -----------------------------------------------
 sunny  mild   high   false
 sunny  cool   normal  false
 rain   mild   normal  false
 sunny  mild   normal  true
 overcast mild   high   true
 overcast hot    normal  false
 rain   mild   high   true  

以上这篇python实现决策树C4.5算法详解(在ID3基础上改进)就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。