详解基于python的全局与局部序列比对的实现(DNA)

程序能实现什么

a.完成gap值的自定义输入以及两条需比对序列的输入
b.完成得分矩阵的计算及输出
c.输出序列比对结果
d.使用matplotlib对得分矩阵路径的绘制

一、实现步骤

1.用户输入步骤

a.输入自定义的gap值
b.输入需要比对的碱基序列1（A,T,C,G）换行表示输入完成
b.输入需要比对的碱基序列2（A,T,C,G）换行表示输入完成

输入（示例）：

2.代码实现步骤

1.获取到用户输入的gap，s以及t
2.调用构建得分矩阵函数，得到得分矩阵以及方向矩阵
3.将得到的得分矩阵及方向矩阵作为参数传到回溯函数中开始回溯得到路径，路径存储使用的是全局变量，存的仍然是方向而不是坐标位置减少存储开销，根据全局变量中存储的方向将比对结果输出。
4.根据全局变量中存储的方向使用matplotlib画出路径

全局比对代码如下：

import matplotlib.pyplot as plt
import numpy as np

#定义全局变量列表finalList存储最后回溯的路径 finalOrder1,finalOrder2存储最后的序列 finalRoad用于存储方向路径用于最后画图
def createList():
  global finalList
  global finalOrder1
  global finalOrder2
  global finalRoad
  finalList = []
  finalOrder1 = []
  finalOrder2 = []
  finalRoad = []

#创建A G C T 对应的键值对，方便查找计分矩阵中对应的得分
def createDic():
  dic = {'A':0,'G':1,'C':2,'T':3}
  return dic
#构建计分矩阵
# A G C T
def createGrade():
  grade = np.matrix([[10,-1,-3,-4],
            [-1,7,-5,-3],
            [-3,-5,9,0],
            [-4,-3,0,8]])
  return grade

#计算两个字符的相似度得分函数
def getGrade(a,b):
  dic = createDic() # 碱基字典 方便查找计分矩阵
  grade = createGrade() # 打分矩阵grade
  return grade[dic[a],dic[b]]

#构建得分矩阵函数 参数为要比较序列、自定义的gap值
def createMark(s,t,gap):
  a = len(s)             #获取序列长度a,b
  b = len(t)
  mark = np.zeros((a+1,b+1))     #初始化全零得分矩阵
  direction = np.zeros((a+1,b+1,3)) #direction矩阵用来存储得分矩阵中得分来自的方向  第一个表示左方 第二个表示左上 第三个表示上方 1表示能往哪个方向去
                    #由于得分可能会来自多个方向，所以使用三维矩阵存储

  direction[0][0] = -1        #确定回溯时的结束条件 即能够走到方向矩阵的值为-1
  mark[0,:] = np.fromfunction(lambda x, y: gap * (x + y), (1, b + 1), dtype=int)   #根据gap值将得分矩阵第一行计算出
  mark[:,0] = np.fromfunction(lambda x, y: gap * (x + y), (1, a + 1), dtype=int)   #根据gap值将得分矩阵第一列计算出
  for i in range(1,b+1):
    direction[0,i,0] = 1
  for i in range(1, a + 1):
    direction[i, 0, 2] = 1

  for i in range(1,a+1):
    for j in range(1,b+1):
      threeMark = [mark[i][j-1],mark[i-1][j-1],mark[i-1][j]]     #threeMark表示现在所要计算得分的位置的左边 左上 上边的得分
      threeGrade = [gap,getGrade(s[i-1],t[j-1]),gap]         #threeGrade表示经过需要计算得左边 左上 上边的空位以及相似度得分
      finalGrade = np.add(threeMark,threeGrade)           #finalGrade表示最终来自三个方向上的得分
      mark[i][j] = max(finalGrade)                  #选取三个方向上的最大得分存入得分矩阵
      #可能该位置的得分可以由多个方向得来，所以进行判断并循环赋值
      for k in range(0,len([y for y,x in enumerate(finalGrade) if x == max(finalGrade)])):
        directionList = [y for y,x in enumerate(finalGrade) if x == max(finalGrade)]
        direction[i][j][directionList[k]] = 1
  return mark,direction

#回溯函数 参数分别为 得分矩阵 方向矩阵 现在所处得分矩阵的位置 以及两个序列
def remount(mark,direction,i,j,s,t):
  if direction[i][j][0] == 1 :
    if direction[i][j-1][0] == -1:      #如果该位置指向左边 先判断其左边是否是零点
      finalList.append(0)          #如果是 将该路径存入路径列表
      finalList.reverse()          #将列表反过来得到从零点开始的路径
      index1 = 0              #记录现在所匹配序列s的位置 因为两个字符串可能是不一样长的
      index2 = 0              #记录现在所匹配序列t的位置
      for k in finalList:
        if k == 0 :
          finalOrder1.append("-")
          finalOrder2.append(t[index2])
          index2 += 1
        if k == 1 :
          finalOrder1.append(s[index1])
          finalOrder2.append(t[index2])
          index1 += 1
          index2 += 1
        if k == 2 :
          finalOrder1.append(s[index1])
          finalOrder2.append("-")
          index1 += 1
      finalList.reverse() # 将原来反转的路径再返回来
      finalRoad.append(np.array(finalList)) # 将此次的路径添加到最终路径记录用于最后画图
      finalList.pop()            #输出后将当前方向弹出 并回溯
      return
    else :
      finalList.append(0)          #如果不是零点 则将该路径加入路径矩阵，继续往下走
      remount(mark,direction,i,j-1,s,t)
      finalList.pop()            #该方向走完后将这个方向弹出 继续下一轮判断 下面两个大的判断同理
  if direction[i][j][1] == 1 :
    if direction[i-1][j-1][0] == -1:

      finalList.append(1)
      finalList.reverse()          # 将列表反过来得到从零点开始的路径
      index1 = 0              # 记录现在所匹配序列s的位置 因为两个字符串可能是不一样长的
      index2 = 0              # 记录现在所匹配序列t的位置
      for k in finalList:
        if k == 0 :
          finalOrder1.append("-")
          finalOrder2.append(t[index2])
          index2 += 1
        if k == 1 :
          finalOrder1.append(s[index1])
          finalOrder2.append(t[index2])
          index1 += 1
          index2 += 1
        if k == 2 :
          finalOrder1.append(s[index1])
          finalOrder2.append("-")
          index1 += 1
      finalList.reverse() # 将原来反转的路径再返回来
      finalRoad.append(np.array(finalList)) # 将此次的路径添加到最终路径记录用于最后画图
      finalList.pop()
      return
    else :
      finalList.append(1)
      remount(mark,direction,i-1,j-1,s,t)
      finalList.pop()
  if direction[i][j][2] == 1 :
    if direction[i-1][j][0] == -1:
      finalList.append(2)
      finalList.reverse()           # 将列表反过来得到从零点开始的路径
      index1 = 0                # 记录现在所匹配序列s的位置 因为两个字符串可能是不一样长的
      index2 = 0                # 记录现在所匹配序列t的位置
      for k in finalList:
        if k == 0 :
          finalOrder1.append("-")
          finalOrder2.append(t[index2])
          index2 += 1
        if k == 1 :
          finalOrder1.append(s[index1])
          finalOrder2.append(t[index2])
          index1 += 1
          index2 += 1
        if k == 2 :
          finalOrder1.append(s[index1])
          finalOrder2.append("-")
          index1 += 1
      finalList.reverse()          # 将原来反转的路径再返回来
      finalRoad.append(np.array(finalList)) # 将此次的路径添加到最终路径记录用于最后画图
      finalList.pop()
      return
    else :
      finalList.append(2)
      remount(mark,direction,i-1,j,s,t)
      finalList.pop()

#画箭头函数
def arrow(ax,sX,sY,aX,aY):
  ax.arrow(sX,sY,aX,aY,length_includes_head=True, head_width=0.15, head_length=0.25, fc='w', ec='b')

#画图函数
def drawArrow(mark, direction, a, b, s, t):
  #a是s的长度为4  b是t的长度为6
  fig = plt.figure()
  ax = fig.add_subplot(111)
  val_ls = range(a+2)
  scale_ls = range(b+2)
  index_ls = []
  index_lsy = []
  for i in range(a):
    if i == 0:
      index_lsy.append('#')
    index_lsy.append(s[a-i-1])
  index_lsy.append('0')
  for i in range(b):
    if i == 0:
      index_ls.append('#')
      index_ls.append('0')
    index_ls.append(t[i])
  plt.xticks(scale_ls, index_ls)      #设置坐标字
  plt.yticks(val_ls, index_lsy)
  for k in range(1,a+2):
    y = [k for i in range(0,b+1)]
    x = [x for x in range(1,b+2)]
    ax.scatter(x, y, c='y')
  for i in range(1,a+2):
    for j in range(1,b+2):
      ax.text(j,a+2-i,int(mark[i-1][j-1]))
  lX = b+1
  lY = 1
  for n in range(0,len(finalRoad)):
    for m in (finalRoad[n]):
      if m == 0:
        arrow(ax,lX,lY,-1,0)
        lX = lX - 1
      elif m == 1:
        arrow(ax,lX,lY,-1,1)
        lX = lX - 1
        lY = lY + 1
      elif m == 2:
        arrow(ax, lX, lY, 0, 1)
        lY = lY + 1
    lX = b + 1
    lY = 1
  ax.set_xlim(0, b + 2) # 设置图形的范围，默认为[0,1]
  ax.set_ylim(0, a + 2) # 设置图形的范围，默认为[0,1]
  ax.set_aspect('equal') # x轴和y轴等比例
  plt.show()
  plt.tight_layout()
if __name__ == '__main__':
  createList()
  print("Please enter gap:")
  gap = int(input())       #获取gap值 转换为整型  tip：刚开始就是因为这里没有进行类型导致后面的计算部分报错
  print("Please enter sequence 1:")
  s = input()           #获取用户输入的第一条序列
  print("Please enter sequence 2:")
  t = input()           #获取用户输入的第二条序列
  a = len(s)           #获取s的长度
  b = len(t)           #获取t的长度
  mark,direction = createMark(s,t,gap)
  print("The scoring matrix is as follows：")     #输出得分矩阵
  print(mark)
  remount(mark,direction,a,b,s,t) #调用回溯函数
  c = a if a > b else b     #判断有多少种比对结果得到最终比对序列的长度
  total = int(len(finalOrder1)/c)
  for i in range(1,total+1):   #循环输出比对结果
    k = str(i)
    print("Sequence alignment results "+k+" is：")
    print(finalOrder1[(i-1)*c:i*c])
    print(finalOrder2[(i-1)*c:i*c])
  drawArrow(mark, direction, a, b, s, t)

局部比对代码如下

import matplotlib.pyplot as plt
import numpy as np
import operator
#在局部比对中 回溯结束的条件是方向矩阵中该位置的值全为0
#定义全局变量列表finalList存储最后回溯的路径 finalOrder1,finalOrder2存储最后的序列
def createList():
  global finalList
  global finalOrder1
  global finalOrder2
  global finalRoad
  finalList = []
  finalOrder1 = []
  finalOrder2 = []
  finalRoad = []

#创建A G C T 对应的键值对，方便查找计分矩阵中对应的得分
def createDic():
  dic = {'A':0,'G':1,'C':2,'T':3}
  return dic
#构建计分矩阵
# A G C T
def createGrade():
  grade = np.matrix([[10,-1,-3,-4],
            [-1,7,-5,-3],
            [-3,-5,9,0],
            [-4,-3,0,8]])
  return grade

#计算两个字符的相似度得分函数
def getGrade(a,b):
  dic = createDic() # 碱基字典 方便查找计分矩阵
  grade = createGrade() # 打分矩阵grade
  return grade[dic[a],dic[b]]

#构建得分矩阵函数 参数为要比较序列、自定义的gap值
def createMark(s,t,gap):
  a = len(s)             #获取序列长度a,b
  b = len(t)
  mark = np.zeros((a+1,b+1))     #初始化全零得分矩阵
  direction = np.zeros((a+1,b+1,3)) #direction矩阵用来存储得分矩阵中得分来自的方向  第一个表示左方 第二个表示左上 第三个表示上方 1表示能往哪个方向去
                    #由于得分可能会来自多个方向，所以使用三维矩阵存
  for i in range(1,a+1):
    for j in range(1,b+1):
      threeMark = [mark[i][j-1],mark[i-1][j-1],mark[i-1][j]]     #threeMark表示现在所要计算得分的位置的左边 左上 上边的得分
      threeGrade = [gap,getGrade(s[i-1],t[j-1]),gap]         #threeGrade表示经过需要计算得左边 左上 上边的空位以及相似度得分
      finalGrade = np.add(threeMark,threeGrade)           #finalGrade表示最终来自三个方向上的得分
      if max(finalGrade) >= 0:                  #如果该最大值是大于0的则 选取三个方向上的最大得分存入得分矩阵 否则不对矩阵进行修改
        mark[i][j] = max(finalGrade)
        for k in range(0,len([y for y,x in enumerate(finalGrade) if x == max(finalGrade)])): #可能该位置的得分可以由多个方向得来，所以进行判断并循环赋值
          directionList = [y for y,x in enumerate(finalGrade) if x == max(finalGrade)]
          direction[i][j][directionList[k]] = 1
  return mark,direction

#回溯函数 参数分别为 得分矩阵 方向矩阵 现在所处得分矩阵的位置 以及两个序列
def remount(mark,direction,i,j,s,t):
  if direction[i][j][0] == 1 :
    if all(direction[i][j-1] == [0,0,0]):      #如果该位置指向左边 先判断其左边是否是零点
      finalList.append(0)          #如果是 将该路径存入路径列表
      finalList.reverse()          #将列表反过来得到从零点开始的路径
      index1 = i              #记录现在所匹配序列s的位置 因为两个字符串可能是不一样长的
      index2 = j-1              #记录现在所匹配序列t的位置
      for k in finalList:
        if k == 0 :
          finalOrder1.append("-")
          finalOrder2.append(t[index2])
          index2 += 1
        if k == 1 :
          finalOrder1.append(s[index1])
          finalOrder2.append(t[index2])
          index1 += 1
          index2 += 1
        if k == 2 :
          finalOrder1.append(s[index1])
          finalOrder2.append("-")
          index1 += 1
      finalList.reverse()
      finalRoad.append(np.array(finalList)) # 将此次的路径添加到最终路径记录用于最后画图
      finalList.pop()            #输出后将当前方向弹出 并回溯
      return
    else :
      finalList.append(0)          #如果不是零点 则将该路径加入路径矩阵，继续往下走
      remount(mark,direction,i,j-1,s,t)
      finalList.pop()            #该方向走完后将这个方向弹出 继续下一轮判断 下面两个大的判断同理
  if direction[i][j][1] == 1 :
    if all(direction[i-1][j-1] == [0,0,0]):
      finalList.append(1)
      finalList.reverse()           # 将列表反过来得到从零点开始的路径
      index1 = i-1              # 记录现在所匹配序列s的位置 因为两个字符串可能是不一样长的
      index2 = j-1              # 记录现在所匹配序列t的位置
      for k in finalList:
        if k == 0 :
          finalOrder1.append("-")
          finalOrder2.append(t[index2])
          index2 += 1
        if k == 1 :
          finalOrder1.append(s[index1])
          finalOrder2.append(t[index2])
          index1 += 1
          index2 += 1
        if k == 2 :
          finalOrder1.append(s[index1])
          finalOrder2.append("-")
          index1 += 1
      finalList.reverse()
      finalRoad.append(np.array(finalList)) # 将此次的路径添加到最终路径记录用于最后画图
      finalList.pop()
      return
    else :
      finalList.append(1)
      remount(mark,direction,i-1,j-1,s,t)
      finalList.pop()
  if direction[i][j][2] == 1 :
    if all(direction[i-1][j] == [0,0,0]):
      finalList.append(2)
      finalList.reverse()           # 将列表反过来得到从零点开始的路径
      index1 = i-1                # 记录现在所匹配序列s的位置 因为两个字符串可能是不一样长的
      index2 = j                # 记录现在所匹配序列t的位置
      for k in finalList:
        if k == 0 :
          finalOrder1.append("-")
          finalOrder2.append(t[index2])
          index2 += 1
        if k == 1 :
          finalOrder1.append(s[index1])
          finalOrder2.append(t[index2])
          index1 += 1
          index2 += 1
        if k == 2 :
          finalOrder1.append(s[index1])
          finalOrder2.append("-")
          index1 += 1
      finalList.reverse()
      finalRoad.append(np.array(finalList)) # 将此次的路径添加到最终路径记录用于最后画图
      finalList.pop()
      return
    else :
      finalList.append(2)
      remount(mark,direction,i-1,j,s,t)
      finalList.pop()
#画箭头函数
def arrow(ax,sX,sY,aX,aY):
  ax.arrow(sX,sY,aX,aY,length_includes_head=True, head_width=0.15, head_length=0.25, fc='w', ec='b')

#画图函数
def drawArrow(mark, direction, a, b, s, t,mx,my):
  #a是s的长度为4  b是t的长度为6
  fig = plt.figure()
  ax = fig.add_subplot(111)
  val_ls = range(a+2)
  scale_ls = range(b+2)
  index_ls = []
  index_lsy = []
  for i in range(a):
    if i == 0:
      index_lsy.append('#')
    index_lsy.append(s[a-i-1])
  index_lsy.append('0')
  for i in range(b):
    if i == 0:
      index_ls.append('#')
      index_ls.append('0')
    index_ls.append(t[i])
  plt.xticks(scale_ls, index_ls)      #设置坐标字
  plt.yticks(val_ls, index_lsy)
  for k in range(1,a+2):
    y = [k for i in range(0,b+1)]
    x = [x for x in range(1,b+2)]
    ax.scatter(x, y, c='y')
  for i in range(1,a+2):
    for j in range(1,b+2):
      ax.text(j,a+2-i,int(mark[i-1][j-1]))
  lX = my + 1
  lY = a - mx + 1
  for n in range(0,len(finalRoad)):
    for m in (finalRoad[n]):
      if m == 0:
        arrow(ax,lX,lY,-1,0)
        lX = lX - 1
      elif m == 1:
        arrow(ax,lX,lY,-1,1)
        lX = lX - 1
        lY = lY + 1
      elif m == 2:
        arrow(ax, lX, lY, 0, 1)
        lY = lY + 1
    lX = b + 1
    lY = 1
  ax.set_xlim(0, b + 2) # 设置图形的范围，默认为[0,1]
  ax.set_ylim(0, a + 2) # 设置图形的范围，默认为[0,1]
  ax.set_aspect('equal') # x轴和y轴等比例
  plt.show()
  plt.tight_layout()

if __name__ == '__main__':
  createList()
  print("Please enter gap:")
  gap = int(input())       #获取gap值 转换为整型  tip：刚开始就是因为这里没有进行类型导致后面的计算部分报错
  print("Please enter sequence 1:")
  s = input()           #获取用户输入的第一条序列
  print("Please enter sequence 2:")
  t = input()           #获取用户输入的第二条序列
  a = len(s)           #获取s的长度
  b = len(t)           #获取t的长度
  mark,direction = createMark(s,t,gap)
  print("The scoring matrix is as follows：")     #输出得分矩阵
  print(mark)
  maxDirection = np.argmax(mark) #获取最大值的位置
  i = int(maxDirection/(b+1))
  j = int(maxDirection - i*(b+1))
  remount(mark,direction,i,j,s,t) #调用回溯函数
  print(finalOrder1)
  print(finalOrder2)
  drawArrow(mark, direction, a, b, s, t, i, j)

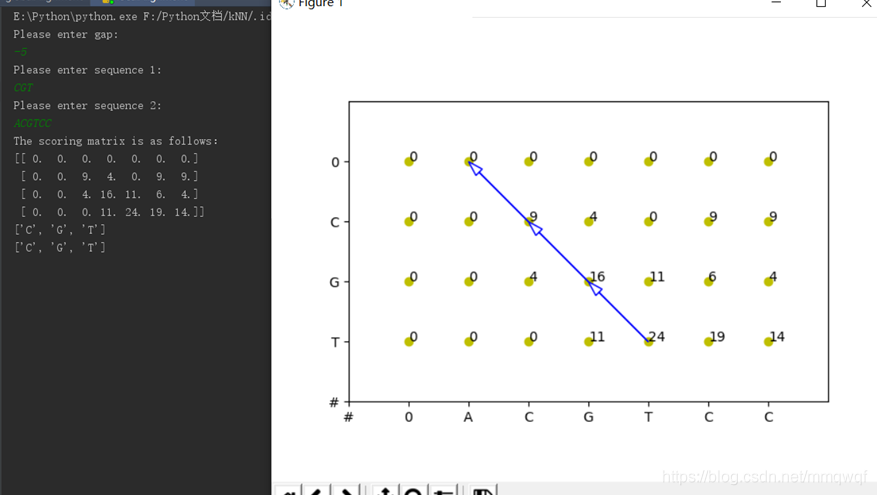
二、实验结果截图

1.全局比对

2.局部比对

到此这篇关于详解基于python的全局与局部序列比对的实现(DNA)的文章就介绍到这了,更多相关python全局与局部序列比对内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

本次实验使用动态规划对全局序列比对进行了实现，自己卡的最久的地方是回溯以及画图的时候。刚开始在实现回溯的过程中，老是找不准回溯的条件以及将所有的路径都记录下来的方法，最后是使用的方向矩阵，也就是重新定义一个与得分矩阵等大的矩阵（但是这个矩阵是三维），存放的是每个位置能够回溯的方向，第一个数值表示左边，第二个表示左上，第三个表示上方，为0时表示当前方向不能回溯，没有路径，为1时表示能回溯，当该位置的所有能走的方向都走完时即可返回。将所有路径记录下来的方法是定义全局变量，当有路径能够走到终点时便将这条路径存放入该全局变量中。
绘图的时候使用的是matplotlib中的散点图，然后将每个点的得分以注释的形式标记在该点的右上角，并用箭头将路径绘出。不得不说的是，这个图确实太丑了，我学识浅薄，也没想到能画出这个图的更好的方法，还希望老师指点。
总的来说这次实验经历的时间还比较长，主要是因为python也没有很熟悉，很多函数也是查了才知道，然后可视化更是了解的少，所以画出来的图出奇的丑，还有回溯的时候也是脑子转不过弯来，所以要学习的东西还有很多，需要更加努力。
本次实验还能够有所改进的地方是：
1.把两个比对算法结合，让用户能够选择使用哪种比对方式。
2.作出一个更好看的界面，增加用户体验感。
3.把图画的更美观。
（老丁已阅，USC的同学们谨慎借鉴）